|
Учебные материалы по физической химии
Задачи по физической химии.Часть 1.Химическая термодинамика
12. Расчет термодинамических функций
идеальных газов статистическими методами
Идеальный газ - удобная модель, для которой
можно точно или с хорошим приближением найти
многие суммы по состояниям и рассчитать
термодинамические функции. Эта модель позволяет
наглядно показать, как статистическая теория
устанавливает связь между внутренним строением
вещества (молекулярными постоянными) и
макроскопическими параметрами
(термодинамическими функциями).
Для расчета термодинамических функций
идеального газа нужно найти логарифм полной
суммы по состояниям. Воспользовавшись связью (11.7)
между полной и молекулярной суммами по
состояниям и разложением (11.8) молекулярной суммы
на сомножители, соответствующие отдельным видам
движения, можно записать:
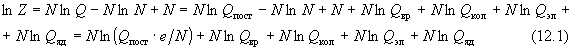
(ln(N!) ~ N lnN - N при больших N). Здесь
логарифм сомножителя 1/N!, который учитывает
неразличимость частиц, объединен с логарифмом
поступательной суммы по состояниям, т.к. именно
поступательное движение обеспечивает эту
неразличимость; в кристаллах, где нет
поступательного движения, все частицы,
фиксированные в центрах кристаллической
решетки, различимы.
Разложение (12.1) позволяет представить любую
термодинамическую функцию идеального газа в
виде суммы вкладов, каждый из которых
соответствует отдельному виду движения:
поступательному, вращательному и т.д. Например,
из (12.1) и (11.3) следует представление молярной
внутренней энергии:
U - U0 = Uпост + Uвр
+ Uкол + Uэл + Uяд,
где
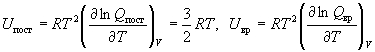 (12.2) (12.2)
и т.д. Мы учли, что kNA = R и
использовали поступательную сумму по состояниям
(11.9).
Аналогичные выражения можно записать для
энергии Гельмгольца и энтропии, если
воспользоваться общими формулами (11.4) и (11.5):
F - U0 = Fпост + Fвр
+ Fкол + Fэл + Fяд,
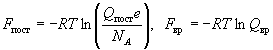 и т.д. (12.3) и т.д. (12.3)
S = Sпост + Sвр + Sкол
+ Sэл + Sяд,
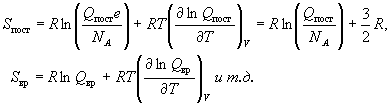 (12.4) (12.4)
Пользуясь формулами (12.2) - (12.4), можно предложить
общую процедуру расчета вклада какого-либо
движения в молярную термодинамическую функцию
идеального газа. Для этого надо взять формулу,
связывающую эту функцию и общую сумму по
состояниям Z, и заменить в этой формуле k
на R, а Z - на Q (или на Q. e/NA
в случае поступательного вклада).
Теорема о распределении по степеням
свободы
В главе 11 мы видели, что во многих случаях сумма
по состояниям представляет собой степенную
функцию температуры. В этих случаях можно
рассчитать вклад такой суммы по состояниям во
внутреннюю энергию и изохорную теплоемкость.
Теорема. Пусть молекулярная сумма по
состояниям для некоторого вида движения имеет
вид:
 , ,
тогда это движение дает следующий вклад в
молярные внутреннюю энергию и изохорную
теплоемкость:
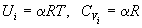 . .
Доказательство.
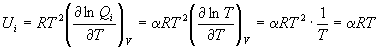 , ,
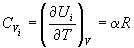
Эту теорему можно использовать для трех видов
движения:
1) поступательное: Qпост ~ T 3/2;
2) вращательное: а) Qвр ~ T 1 для
линейных молекул,
б) Qвр ~ T 3/2 для нелинейных
молекул;
3) колебательное: для каждого колебания Qкол
~ T 1, если T >> Tкол.
Если при некоторой температуре сумма по
состояниям для какого-либо вида движения близка
к 1, то вклад этого вида движения в любые
термодинамические функции мал, и оно называется замороженным
при данной температуре.
ПРИМЕРЫ
Пример 12-1. Поступательный вклад в энтропию
углекислого газа при некоторых условиях равен
148.5 Дж/(моль. К). Рассчитайте поступательный
вклад в энтропию кислорода при этих же условиях.
Решение. Поступательный вклад в энтропию
описывается формулой (12.4). Достаточно найти
зависимость этого вклада только от молярной
массы газа, т.к. температура и объем для двух
газов, по условию, одинаковы. Поступательная
сумма по состояниям Qпост ~ M3/2
(это следует из (11.9)), поэтому
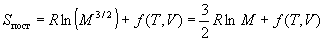 , ,
где f(T,V) - функция, которая не зависит
от молярной массы. Отсюда следует:
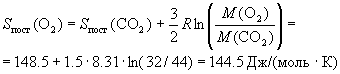 . .
Ответ. 144.5 Дж/(моль К).
Пример 12-2. Рассчитайте молярные энтропию,
внутреннюю энергию, энтальпию, энергии
Гельмгольца и Гиббса газообразного азота при T
= 298 K и давлении 1 атм. Вращательная постоянная B
= 2.00 см-1, колебательная частота  = 2360 см-1. Электронной и
ядерной составляющими пренебречь. = 2360 см-1. Электронной и
ядерной составляющими пренебречь.
Решение. Колебательным вкладом здесь можно
пренебречь, т.к. температура T = 298 К намного
меньше эффективной колебательной температуры Tкол
= hc / k = 3400 К. / k = 3400 К.
Рассчитаем поступательную и вращательную
суммы по состояниям:
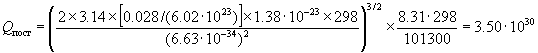
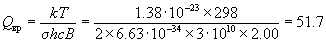
Внутреннюю энергию можно найти по теореме о
распределении по степеням свободы:
U - U0 = Uпост + Uвр =
3/2 RT + RT = 5/2 RT = 6191 Дж/моль,
молярную энтальпию - по определению H = U +
pV:
H - U0 = U - U0 + pV = U -
U0 + RT = 7/2 RT = 8667 Дж/моль.
Молярную энтропию находим по формулам (12.4):
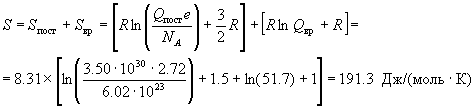 , ,
а энергии Гельмгольца и Гиббса - по
определениям F = U - TS и G = F + pV:
F - U0 = U - U0 - TS = 6191 -
298 191.3 = -50820 Дж/моль, 191.3 = -50820 Дж/моль,
G - U0 = F - U0 + RT = -50820
+ 8.31 298 = -48340 Дж/моль. 298 = -48340 Дж/моль.
Пример 12-3. Оцените мольную теплоемкость CV
газообразного метана при комнатной температуре.
(Экспериментальное значение: 27.2 Дж/(моль.
К).)
Решение. Колебательным вкладом в
теплоемкость пренебрегаем, т.к. при комнатной
температуре T ~ 298 К все колебания заморожены.
Вклад вращательного и поступательного движений
находим по теореме о распределении по степеням
свободы:
Qпост ~ T 3/2, 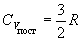 , ,
Qвр ~ T 3/2 (нелинейная
молекула), 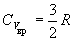 , ,
CV = 3/2 R + 3/2 R = 3R = 25 Дж/(моль.
К).
Ответ. 25 Дж/(моль К).
ЗАДАЧИ
12-1. Рассчитайте поступательный вклад в
энтропию молекулярного хлора при температуре 20 оС
и давлении 1 атм.
12-2. Рассчитайте поступательный вклад в
энтропию газообразного кислорода при
температуре -10 оС и давлении 1.1 атм.
12-3. Рассчитайте вращательный вклад в
энтропию оксида углерода (II) при температуре 200 оС.
Вращательная постоянная CO равна: B = 1.93 см-1.
12-4. Рассчитайте вращательный вклад в
энтропию бромоводорода при температуре 100 оС.
Вращательная постоянная B = 8.47 см-1.
12-5. Поступательный вклад в энтропию водорода
при некоторых условиях равен 108.0 Дж/(моль.
К), а в энтропию неизвестного газа при этих же
условиях - 147.1 Дж/(моль. К). Определите
неизвестный газ.
12-6. Вращательный вклад в энтропию CO при
некоторой температуре равен 51.5 Дж/(моль. К).
Чему равен вращательный вклад в энтропию O2
при этой температуре? Вращательные постоянные: CO
- 1.93 см-1, O2 - 1.45 см-1.
12-7. Вращательный вклад в энтропию CO при
температуре 500 К равен 51.5 Дж/(моль. К). Чему
равен этот вклад при комнатной температуре (293 К)?
12-8. Вращательный вклад в энтропию некоторого
газа (молекула - линейная) при комнатной
температуре (293 К) равен 33.7 Дж/(моль. К). Чему
равен этот вклад при температуре 450 К?
12-9. Рассчитайте колебательный вклад в
энтропию и изохорную теплоемкость газообразного
фтора ( = 917 см-1) при
температурах 298 и 1273 К. = 917 см-1) при
температурах 298 и 1273 К.
12-10. Рассчитайте мольные энтропию, внутреннюю
энергию, энтальпию, энергии Гельмгольца и Гиббса
газообразного аргона при T = 298 K и давлении 1
атм.
12-11. Рассчитайте мольные энтропию, внутреннюю
энергию, энтальпию, энергии Гельмгольца и Гиббса
газообразного молекулярного иода при T = 500 K и
давлении 5 атм. Вращательная постоянная B = 0.0374
см-1, частота колебаний  =
214 см-1. =
214 см-1.
12-12. Оцените мольную теплоемкость CP
газообразного этилена при комнатной
температуре.
12-13. Оцените мольную теплоемкость CV
газообразного NO2 при комнатной
температуре.
12-14. Оцените мольную теплоемкость CP
газообразного CO при комнатной температуре.
12-15. Оцените мольную теплоемкость CV
газообразного озона при комнатной температуре.
12-16. Оцените мольную теплоемкость CP
газообразного SO2 при температуре 2000 K.
12-17. Сравните мольные теплоемкости
газообразных воды и углекислого газа при 300 K в
предположении, что вкладами электронных и
колебательных движений можно пренебречь.
12-18. Не проводя вычислений, сравните
теплоемкости CV оксида азота N2O и
оксида углерода CO2 при 298 K с использованием
следующих молекулярных постоянных:
12-19. У какого из газов - кислорода или
углекислого газа - больше энтропия при
одинаковых условиях? Объясните, почему.
|

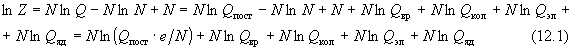
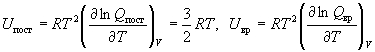 (12.2)
(12.2)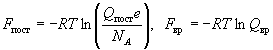 и т.д. (12.3)
и т.д. (12.3)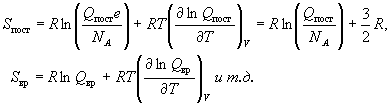 (12.4)
(12.4)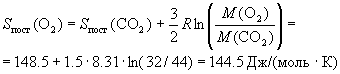 .
.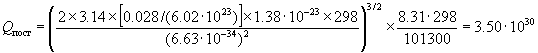
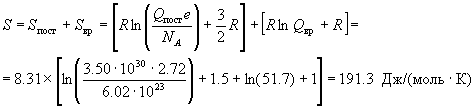 ,
,