|
Учебные материалы по физической химии
Реальные газы
1.3. Уравнение Ван-дер-Ваальса
Предпринималось много попыток для учета
отклонений свойств реальных газов от свойств
идеального газа путем введения различных
поправок в уравнение состояния идеального газа.
Наибольшее распространение вследствие простоты
и физической наглядности получило уравнение
Ван-дер-Ваальса (1873).
Первая поправка в уравнении состояния
идеального газа рассматривает собственный
объем, занимаемый молекулами реального газа. В
уравнении Дюпре (1864)
p (V – nb) = nRT (1.3)
постоянная b учитывает собственный мольный
объем молекул.
При понижении температуры межмолекулярное
взаимодействие в реальных газах приводит к
конденсации (образование жидкости).
Межмолекулярное притяжение эквивалентно
существованию в газе некоторого внутреннего
давления  (иногда его
называют статическим давлением). Изначально
величина (иногда его
называют статическим давлением). Изначально
величина  была учтена в
общей форме в уравнении Гирна (1865) была учтена в
общей форме в уравнении Гирна (1865)
(p +  ) (V – nb) = nRT.
(1.4) ) (V – nb) = nRT.
(1.4)
Ван-дер-Ваальс в 1873 г. дал функциональную
интерпретацию внутреннего давления. Согласно
модели Ван-дер-Ваальса, силы притяжения между
молекулами (силы Ван-дер-Ваальса) обратно
пропорциональны шестой степени расстояния между
ними, или второй степени объема, занимаемого
газом. Считается также, что силы притяжения
суммируются с внешним давлением. С учетом этих
соображений уравнение состояния идеального газа
преобразуется в уравнение Ван-дер-Ваальса:
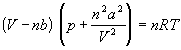 (1.5) (1.5)
или для одного моля
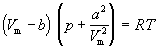 . (1.6) . (1.6)
Значения постоянных Ван-дер-Ваальса a и b,
которые зависят от природы газа, но не зависят от
температуры, приведены в таблице 1.3.
Таблица 1.3. Постоянные
Ван-дер-Ваальса для различных газов
| Газ |
a, л2 *бар* моль-2 |
b,см3 * моль-1 |
Газ |
a, л2 * бар* моль-2 |
b, см3 * моль-1 |
| He |
0,03457 |
23,70 |
NO |
1,358 |
27,89 |
| Ne |
0,2135 |
17,09 |
NO2 |
5,354 |
44,24 |
| Ar |
1,363 |
32,19 |
H2O |
5,536 |
30,49 |
| Kr |
2,349 |
39,78 |
H2S |
4,490 |
42,87 |
| Xe |
4,250 |
51,05 |
NH3 |
4,225 |
37,07 |
| H2 |
0,2476 |
26,61 |
SO2 |
6,803 |
56,36 |
| N2 |
1,408 |
39,13 |
CH4 |
2,283 |
42,78 |
| O2 |
1,378 |
31,83 |
C2H4 |
4,530 |
5,714 |
| Cl2 |
6,579 |
56,22 |
C2H6 |
5,562 |
63,80 |
| CO |
1,505 |
39,85 |
C3H8 |
8,779 |
84,45 |
| CO2 |
3,640 |
42,67 |
C6H6 |
18,24 |
115,4 |
Уравнение (1.6) можно переписать так, чтобы
выразить в явном виде давление
 (1.7) (1.7)
или объем
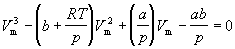 (1.8) (1.8)
Уравнение (1.8) содержит объем в третьей степени
и, следовательно, имеет или три действительных
корня, или один действительный и два мнимых. При
высоких температурах уравнение (1.8) имеет один
действительный корень, и по мере повышения
температуры кривые, вычисленные по уравнению
Ван-дер-Ваальса, приближаются к гиперболам,
соответствующим уравнению состояния идеального
газа.
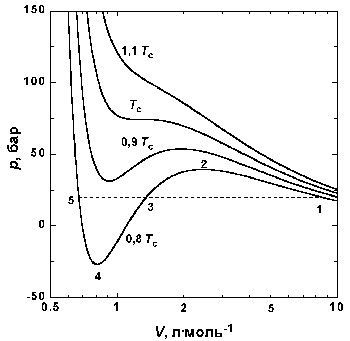 |
| Рис.1.4 Изотермы Ван-дер-Ваальса
для СО2 |
На рис. 1.4 (стр. 7) приведены изотермы,
вычисленные по уравнению Ван-дер-Ваальса для
диоксида углерода (значения констант a и b
взяты из табл. 1.3). Из рисунка видно, что при
температурах ниже критической (31,04 °С) вместо
горизонтальных прямых, соответствующих
равновесию жидкости и пара, получаются
волнообразные кривые 12345 с тремя действительными
корнями, из которых только два, 1 и 5, физически
осуществимы. Третий корень (точка 3) физически не
реален, поскольку находится на участке кривой 234,
противоречащем условию стабильности
термодинамической системы 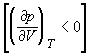 . Состояния на участках 12 и 54, которые
соответствуют переохлажденному пару и
перегретой жидкости, соответственно, являются
неустойчивыми (метастабильными) и могут быть
лишь частично реализуемы в специальных
условиях. Так, осторожно сжимая пар выше точки 1
(рис. 1.4), можно подняться по кривой 12. Для этого
необходимо отсутствие в паре центров
конденсации, и в первую очередь пыли. В этом
случае пар оказывается в пересыщенном, т.е.
переохлажденном состоянии. И наоборот,
образованию капелек жидкости в таком паре
способствуют, например, попадающие в него ионы.
Это свойство пересыщенного пара используется в
известной камере Вильсона (1912), применяемой для
регистрации заряженных частиц. Движущаяся
заряженная частица, попадая в камеру, содержащую
пересыщенный пар, и соударяясь с молекулами,
образует на своем пути ионы, создающие туманный
след – трек, который фиксируется фотографически. . Состояния на участках 12 и 54, которые
соответствуют переохлажденному пару и
перегретой жидкости, соответственно, являются
неустойчивыми (метастабильными) и могут быть
лишь частично реализуемы в специальных
условиях. Так, осторожно сжимая пар выше точки 1
(рис. 1.4), можно подняться по кривой 12. Для этого
необходимо отсутствие в паре центров
конденсации, и в первую очередь пыли. В этом
случае пар оказывается в пересыщенном, т.е.
переохлажденном состоянии. И наоборот,
образованию капелек жидкости в таком паре
способствуют, например, попадающие в него ионы.
Это свойство пересыщенного пара используется в
известной камере Вильсона (1912), применяемой для
регистрации заряженных частиц. Движущаяся
заряженная частица, попадая в камеру, содержащую
пересыщенный пар, и соударяясь с молекулами,
образует на своем пути ионы, создающие туманный
след – трек, который фиксируется фотографически.
Согласно правилу Максвелла (the Maxwell construction),
которое имеет теоретическое обоснование, для
того, чтобы расчетная кривая соответствовала
экспериментальной равновесной изотерме, нужно
вместо кривой 12345 провести горизонтальную прямую
15 так, чтобы площади 1231 и 3453 были равны. Тогда
ордината прямой 15 будет равна давлению
насыщенного пара, а абсциссы точек 1 и 5 – мольным
объемам пара и жидкости при данной температуре.
По мере повышения температуры все три корня
сближаются, и при критической температуре Tc
все три корня становятся равными. В критической
точке изотерма Ван-дер-Ваальса имеет точку
перегиба [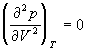 ] с
горизонтальной касательной [ ] с
горизонтальной касательной [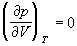 ], то есть ], то есть
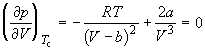 , (1.9) , (1.9)
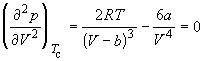 . (1.10) . (1.10)
Совместное решение этих уравнений дает:
 , (1.11) , (1.11)
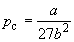 , (1.12) , (1.12)
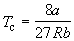 , (1.13) , (1.13)
что позволяет определять константы уравнения
Ван-дер-Ваальса из критических параметров газа.
Соответственно, согласно уравнению
Ван-дер-Ваальса, критический фактор
сжимаемости Zc для всех газов должен
быть равен
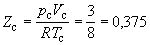 (1.14) (1.14)
Из таблицы 1.2 видно, что хотя значение Zc
для реальных газов приблизительно постоянно (0,27
– 0,30 для неполярных молекул), оно все же заметно
меньше вытекающего из уравнения Ван-дер-Ваальса.
Для полярных молекул наблюдается еще большее
расхождение.
Принципиальное значение уравнения
Ван-дер-Ваальса определяется следующими
обстоятельствами:
1) уравнение было получено из модельных
представлений о свойствах реальных газов и
жидкостей, а не явилось результатом
эмпирического подбора функции f(p,V,T),
описывающей свойства реальных газов;
2) уравнение долго рассматривалось как
некоторый общий вид уравнения состояния
реальных газов, на основе которого было
построено много других уравнений состояния (см.
ниже);
3) с помощью уравнения Ван-дер-Ваальса впервые
удалось описать явление перехода газа в жидкость
и проанализировать критические явления. В этом
отношении уравнение Ван-дер-Ваальса имеет
преимущество даже перед более точными
уравнениями в вириальной форме (см. 1.1, 1.2).
Причиной недостаточной точности уравнения
Ван-дер-Ваальс считал ассоциацию молекул в
газовой фазе, которую не удается описать,
учитывая зависимость параметров a и b от
объема и температуры, без использования
дополнительных постоянных. После 1873 г. сам
Ван-дер-Ваальс предложил еще шесть вариантов
своего уравнения, последнее из которых относится
к 1911 г. и содержит пять эмпирических постоянных.
Две модификации уравнения (1.5) предложил
Клаузиус, и обе они связаны с усложнением вида
постоянной b. Больцман получил три уравнения
этого типа, изменяя выражения для постоянной a.
Всего известно более сотни подобных уравнений,
отличающихся числом эмпирических постоянных,
степенью точности и областью применимости.
Выяснилось, что ни одно из уравнений состояния,
содержащих менее 5 индивидуальных постоянных, не
оказалось достаточно точным для описания
реальных газов в широком диапазоне p, V, T, и все
эти уравнения оказались непригодными в области
конденсации газов. Из простых уравнений с двумя
индивидуальными параметрами неплохие
результаты дают уравнения Дитеричи и Бертло (см.
табл. 1.4).
|

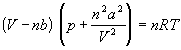 (1.5)
(1.5)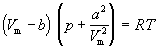 . (1.6)
. (1.6)
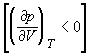 . Состояния на участках 12 и 54, которые
соответствуют переохлажденному пару и
перегретой жидкости, соответственно, являются
неустойчивыми (метастабильными) и могут быть
лишь частично реализуемы в специальных
условиях. Так, осторожно сжимая пар выше точки 1
(рис. 1.4), можно подняться по кривой 12. Для этого
необходимо отсутствие в паре центров
конденсации, и в первую очередь пыли. В этом
случае пар оказывается в пересыщенном, т.е.
переохлажденном состоянии. И наоборот,
образованию капелек жидкости в таком паре
способствуют, например, попадающие в него ионы.
Это свойство пересыщенного пара используется в
известной камере Вильсона (1912), применяемой для
регистрации заряженных частиц. Движущаяся
заряженная частица, попадая в камеру, содержащую
пересыщенный пар, и соударяясь с молекулами,
образует на своем пути ионы, создающие туманный
след – трек, который фиксируется фотографически.
. Состояния на участках 12 и 54, которые
соответствуют переохлажденному пару и
перегретой жидкости, соответственно, являются
неустойчивыми (метастабильными) и могут быть
лишь частично реализуемы в специальных
условиях. Так, осторожно сжимая пар выше точки 1
(рис. 1.4), можно подняться по кривой 12. Для этого
необходимо отсутствие в паре центров
конденсации, и в первую очередь пыли. В этом
случае пар оказывается в пересыщенном, т.е.
переохлажденном состоянии. И наоборот,
образованию капелек жидкости в таком паре
способствуют, например, попадающие в него ионы.
Это свойство пересыщенного пара используется в
известной камере Вильсона (1912), применяемой для
регистрации заряженных частиц. Движущаяся
заряженная частица, попадая в камеру, содержащую
пересыщенный пар, и соударяясь с молекулами,
образует на своем пути ионы, создающие туманный
след – трек, который фиксируется фотографически.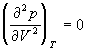 ] с
горизонтальной касательной [
] с
горизонтальной касательной [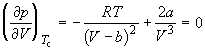 , (1.9)
, (1.9)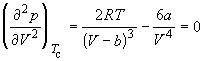 . (1.10)
. (1.10)