4.2. Эксергия материальных потоков
4.2.1. Полная работа в технологической системе
Вернемся к схематическому представлению технологической системы как
"черного ящика", в котором происходит преобразование материального
потока из состояния "1" в состояние "2",
сопровождаемое производством (потреблением) работы и теплообменом с внешним
источником (стоком) тепловой энергии. В стационарном режиме функционирования
системы потоки энергии связаны уравнением баланса (3.8) или его упрощенной
версией (3.9). Для периодического процесса то же уравнение остается
справедливым после осреднения потоков по периоду процесса.
Заданное преобразование потока вещества 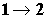 может быть осуществлено многообразными
способами, каждый из которых будет характеризоваться как соотношением потоков может быть осуществлено многообразными
способами, каждый из которых будет характеризоваться как соотношением потоков 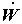 и и 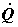 , так и потенциалом
переносимой теплоты, при фиксированном суммарном потоке , так и потенциалом
переносимой теплоты, при фиксированном суммарном потоке  . Поскольку в нашем распоряжении
имеется термодинамический метод сравнения энергетической ценности потоков
теплоты и работы, то суммарный поток энергии может быть приведен к единому
энергетическому эквиваленту. . Поскольку в нашем распоряжении
имеется термодинамический метод сравнения энергетической ценности потоков
теплоты и работы, то суммарный поток энергии может быть приведен к единому
энергетическому эквиваленту.

Рис. 4.5. Схема получения в
технологической системе дополнительной работы с помощью тепловой машины.
В уравнении баланса энергии 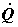 обозначает поток теплоты в систему.
Соответственно, тепловой поток из системы равен обозначает поток теплоты в систему.
Соответственно, тепловой поток из системы равен  (действительное направление потока
определяется тем, какая из этих двух величин положительна). Пусть теплота
отводится от системы (подводится к ней) при температуре T .
Передавая теплоту (действительное направление потока
определяется тем, какая из этих двух величин положительна). Пусть теплота
отводится от системы (подводится к ней) при температуре T .
Передавая теплоту  машине Карно, действующей между системой и окружающей средой,
(см. рис.4.5) можно получить дополнительное количество работы машине Карно, действующей между системой и окружающей средой,
(см. рис.4.5) можно получить дополнительное количество работы  . Эта работа выражается
соотношением (4.5), но с учетом того, что положительное направление потока
теплоты определено теперь по отношению к исследуемой технологической системе,
т.е. . Эта работа выражается
соотношением (4.5), но с учетом того, что положительное направление потока
теплоты определено теперь по отношению к исследуемой технологической системе,
т.е.
 . (4.6) . (4.6)
Если система поглощает теплоту, (4.6) характеризует эквивалентные затраты
работы. Полная работа системы выразится суммой
 , (4.7) , (4.7)
зависящей от траектории перехода 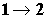 . Понятие полной работы в указанном смысле
введено Р.Хейвудом; индекс g есть сокращение от gross. . Понятие полной работы в указанном смысле
введено Р.Хейвудом; индекс g есть сокращение от gross.
Напомним, что степень трансформации теплоты в работу, выражаемая
соотношением (4.5), отвечает идеализированным (равновесным) условиям
функционирования машины Карно. Следовательно, (4.6) характеризует
максимальную эквивалентную работу  в случае отвода теплоты от системы и минимальные
эквивалентные затраты работы в случае подвода теплоты к системе. в случае отвода теплоты от системы и минимальные
эквивалентные затраты работы в случае подвода теплоты к системе.
Сложение работы и переведенной в работу теплоты есть вынужденный шаг, если
мы не хотим ограничиться анализом строго адиабатных процессов – траектории
таких процессов, очевидно, могут быть сопоставлены по величине чистой работы 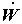 . Функция полной
работы . Функция полной
работы  дает
возможность сопоставлять по термодинамической эффективности возможные
траектории любого технологического процесса. Ясно, что предпочтительными
являются те траектории, которые обеспечивают более высокие значения дает
возможность сопоставлять по термодинамической эффективности возможные
траектории любого технологического процесса. Ясно, что предпочтительными
являются те траектории, которые обеспечивают более высокие значения  , если система
отдает энергию, и меньшие по абсолютной величине значения , если система
отдает энергию, и меньшие по абсолютной величине значения  , если система потребляет
энергию. , если система потребляет
энергию.
Соотношения (4.6) и (4.7) нетрудно обобщить на такую ситуацию, когда в
теплообмен вступают части системы, имеющие разные температуры (см. раздел 2.1).
Пусть от i-ой подсистемы с температурой Ti
отводится поток теплоты  . Присоединяя каждую из подсистем к
отдельной машине Карно, можно получить в сумме дополнительную работу . Присоединяя каждую из подсистем к
отдельной машине Карно, можно получить в сумме дополнительную работу
 . (4.8) . (4.8)
Отсюда полная работа с учетом равенства  выразится как выразится как
 . (4.9) . (4.9)
В общем случае суммы в правой части (4.8) и (4.9) должны быть заменены на
интегралы от переменного вектора потока теплоты по всей поверхности,
ограничивающей систему. Однако, такое уточнение нисколько не изменяет
окончательный вид полученных далее (раздел 4.2.3) интегральных уравнений баланса
энергии.
|

