Вариант 25

1.

2. Второй вириальный коэффициент для газа частиц с центральным взаимодействием определяется уравнением:

B₂(T) = 2N_A {1- exp[-f(r)/kT]} r²dr.

Имеем:

B₂(T) = (2N_A³/3) + 2N_A [1 - exp(⁶/r⁶kT)] r²dr.

Вводя новую переменную интегрирования (r/)³ = x, получаем:

B₂(T) = (2N_A³/3) + (2N_A³/3) [1 - exp(/x²kT)] dx.

Раскладывая экспоненциальную функцию в ряд, и выполняя почленное интегрирование ряда, получаем:

[1 - exp( /x²kT)] dx.= -(1/n!)(/ kT)ⁿ (1/x²ⁿ)] dx = -(/ kT)ⁿ [1/n!(2n-1)].

Таким образом,

B₂(T) = (2N_A³/3) - (2N_A³/3) (/ kT)ⁿ [1/n!(2n-1)].

3.

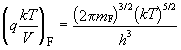
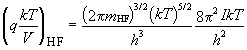
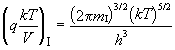
= D_HF - D_HI = 566.3 - 294.6 = 271.7 кДж/моль

lnK_p = 1.1 -32680/T

lnK_p(298) = -108

G⁰ = -RT lnK_p = -9.15T + 217700

G⁰(298) = 216270 Дж/моль

S⁰ = -( G/T)_p = 9.15 Дж/(моль^. К)

S⁰(298) = 9.15 Дж/(моль^. К)

H⁰ = G + TS = 217700 Дж/моль

H⁰(298) = 217700 Дж/моль