|
Учебные материалы по физической химии
Реальные газы
2.3. Модельные представления о реальных
газах
Реальные газы отличаются от идеальных
тем, что частицы имеют собственный объем, а
потенциал взаимодействия отличен от 0.
Рассмотрим две простые модели, которые позволят
учесть эти факторы при расчете статистической
суммы газа.
2.3.1. Модель решеточного газа
В модели решеточного газа предполагается,
что N различимых частиц движутся в объеме V,
разделенном на ячейки объемом b, при этом
число ячеек n = V / b предполагается
намного большим, чем число частиц, т.е.
большинство ячеек - пустые (рис. 2.1). В каждой
ячейке может находиться не более одной частицы
(если в одной ячейке находятся две частицы, то
потенциальная энергия принимается равной +Ґ ).
Частицы, находящиеся в разных ячейках, не
взаимодействуют, т.е. потенциальная энергия
равна 0. Фактически, в этой модели объем ячейки -
это собственный объем частиц. Найдем уравнение
состояния для решеточного газа.
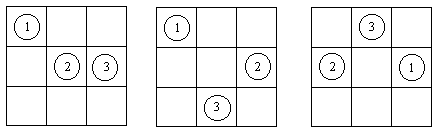
Рис. 2.1. Три из 504 вариантов расположения трех
различимых частиц в 9 ячейках.
Для вычисления конфигурационного интеграла
рассмотрим какое-либо конкретное разбиение N
частиц по n ячейкам. Интегрирование по
координатам каждой частицы в (2.8) даст объем
ячейки b, а таких частиц - N штук, поэтому
вклад данного разбиения частиц по ячейкам в
конфигурационный интеграл равен bN.
Число разбиений N частиц по n ячейкам
равно nЧ (n–1)...(n–N+1) = 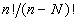 , поскольку первая частица может
занимать n ячеек, вторая - (n–1) ячеек, а N-ая
частица - (n–N+1) ячеек. Конфигурационный
интеграл решеточного газа равен , поскольку первая частица может
занимать n ячеек, вторая - (n–1) ячеек, а N-ая
частица - (n–N+1) ячеек. Конфигурационный
интеграл решеточного газа равен
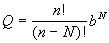 (2.12) (2.12)
Для оценки давления используем естественные
приближения: 1) N >> 1, т.к. число частиц в газе
велико (порядка 1023); 2) n >> N, т.к.
общий объем газа nb намного больше общего
собственного объема частиц Nb.
Воспользовавшись формулой Стирлинга
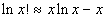 при больших x, при больших x,
получим следующее выражение:
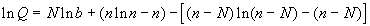
Уравнение состояния получаем с помощью (2.9) с
учетом того, что V = nb:
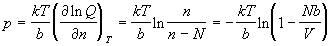 . (2.13) . (2.13)
В принципе, полученная формула решает задачу.
Далее, можно представить уравнение состояния (2.13)
в вириальном виде, воспользовавшись разложением
логарифма по малому параметру (Nb/V):
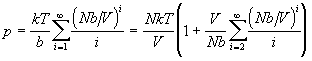 , ,
откуда следует, что i-й вириальный
коэффициент равен:
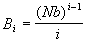 . .
В частности, второй вириальный коэффициент
равен половине общего собственного объема
молекул:
B2 = Nb / 2 .
Из уравнения состояния (2.13) следует, что 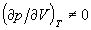 при любых объемах. Это
означает, что решеточный газ без
взаимодействия ни при каких условиях не
проявляет критического поведения и наличие
собственного объема, которое можно
рассматривать как существование бесконечного
отталкивания на малых расстояниях, само по себе
не может приводить к конденсации газа. при любых объемах. Это
означает, что решеточный газ без
взаимодействия ни при каких условиях не
проявляет критического поведения и наличие
собственного объема, которое можно
рассматривать как существование бесконечного
отталкивания на малых расстояниях, само по себе
не может приводить к конденсации газа.
2.3.2. Модель решеточного газа с
взаимодействием
Для того, чтобы оценить роль межчастичного
взаимодействия в поведении реальных газов,
рассмотрим модель решеточного газа с
притяжением, в котором каждая пара частиц
взаимодействует друг с другом с одинаковым
потенциалом, равным –2a/V, где a -
постоянная, V - объем газа. Объем введен в
знаменатель, чтобы учесть зависимость общей
энергии взаимодействия от среднего расстояния
между молекулами (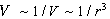 ). ).
В этом случае общий потенциал взаимодействия
всех частиц не зависит от конфигурации (т.е., от
распределения частиц по ячейкам) и равен
произведению парного потенциала на число пар
частиц:
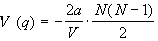 . .
Этот потенциал приводит к появлению множителя
exp(–V/kT) в конфигурационном интеграле:
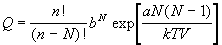 . (2.14) . (2.14)
Дифференцируя lnQ по объему и учитывая, что N
(N–1) ~ N2, получим термическое
уравнение состояния решеточного газа с
притяжением:
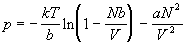 . (2.15) . (2.15)
Второй вириальный коэффициент для этого газа
равен
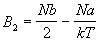 . .
При температуре T = 2a/kb (температуре
Бойля) коэффициент B2 обращается в 0 и
поведение газа близко к идеальному, т.к. эффект
притяжения при температуре Бойля в некотором
смысле уравновешивает эффект отталкивания.
Найдем калорическое уравнение состояния,
которое определяется зависимостью
статистической суммы от температуры. Для данной
модели эта зависимость имеет вид (см. (2.7), (2.8), (2.14)):
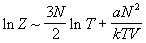 , ,
откуда находим внутреннюю энергию:
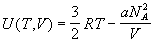 . .
Точно так же зависит от температуры и объема
внутренняя энергия одноатомного газа
Ван-дер-Ваальса. Таким образом, калорические
уравнения состояния решеточного газа с
взаимодействием и газа Ван-дер-Ваальса совпадают
друг с другом. Теплоемкость решеточного газа
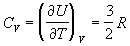
равна теплоемкости одноатомного идеального
газа.
Убедимся в том, что данная модель газа
описывает критическое поведение. Критические
параметры для этой модели реального газа найдем
из соотношений:
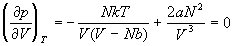 , ,
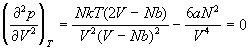 . .
Исключая температуру, находим критический
объем:
Vc = 2Nb.
Критическая температура равна:
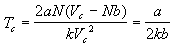 . .
Критическое давление можно найти из уравнения
состояния (2.15):
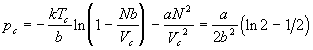 . .
Если в этой модели пренебречь собственным
объемом частиц, т.е. устремить b к 0, то
критический объем также устремится к 0, а
критические температура и давление - к
бесконечности. Это означает, что критического
поведения не будет.
Критический фактор сжимаемости равен (не
путать обозначение со статсуммой):
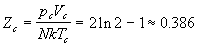 , ,
что очень близко к аналогичному значению 3/8 = 0.375
для газа Ван-дер-Ваальса.
Главный вывод, который следует из рассмотрения
двух моделей решеточного газа состоит в том, что критические
явления в реальном газе могут появляться только
в том случае, когда потенциал взаимодействия
содержит как отталкивательную часть (на малых, но
конечных расстояниях), так и притягивающую часть.
|


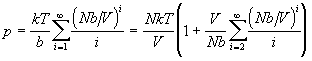 ,
,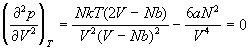 .
.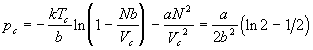 .
.