Глава 2. Производство энтропии – количественная мера неравновесности процесса
2.1. Второе начало термодинамики
В курсах физической химии обсуждение второго начала термодинамики
сосредотачивается на том, что этим законом устанавливается общая направленность
макроскопических процессов в природе. Второе начало "запрещает"
протекание одних процессов и "разрешает" осуществление противоположно
направленных процессов. В настоящем курсе в интерпретации второго начала
оттеняется его конструктивное значение для синтеза технологических систем,
заключающееся в том, что законом определяется та категория процессов (это – равновесные,
или точнее, квазиравновесные процессы), в которых преобразование материальных
потоков протекает при наиболее полноценном использовании энергии в ее разных
формах.
Будем исходить из формулировки второго начала термодинамики в виде
неравенства Клаузиуса
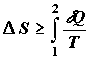 . (2.1) . (2.1)
Вопрос заключается в приспособленной для анализа технологических процессов
трактовке этого неравенства. В стационарном режиме процесса происходит изменение
состояния совокупного материального потока, проходящего через систему. А
именно, состояние каждой перерабатываемой порции вещества изменяется от ее
первоначального состояния "1" в виде исходных реагентов до
конечного состояния "2" в виде продуктов процесса. В то же
время внутреннее состояние технологической системы (состояние "черного
ящика" – в соответствии с обобщенной моделью в Главе 1) сохраняется
неизменным. Аналогично в периодическом технологическом процессе после
завершения полного цикла мы наблюдаем только изменение состояния совокупности
произведенных продуктов по отношению к израсходованным исходным реагентам;
состояние самой системы по завершении цикла возвращается в первоначальное.
Таким образом под 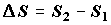 в неравенстве (2.1) будем понимать изменение энтропии
совокупности рабочих веществ в ходе технологического процесса (соответственно
за любой конечный временной интервал – в стационарном процессе и за полный технологический
цикл – в периодическом процессе); T – термодинамическая температура,
физический смысл которой устанавливается из анализа цикла Карно; в неравенстве (2.1) будем понимать изменение энтропии
совокупности рабочих веществ в ходе технологического процесса (соответственно
за любой конечный временной интервал – в стационарном процессе и за полный технологический
цикл – в периодическом процессе); T – термодинамическая температура,
физический смысл которой устанавливается из анализа цикла Карно; 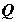 – элементарная порция
теплоты, передаваемая системе при текущем значении температуры T, вообще
говоря, переменной по времени и пространственным координатам. Знак равенства в
(2.1) относится к равновесным переходам из состояния "1" в
состояние "2"; знак неравенства – к неравновесным. – элементарная порция
теплоты, передаваемая системе при текущем значении температуры T, вообще
говоря, переменной по времени и пространственным координатам. Знак равенства в
(2.1) относится к равновесным переходам из состояния "1" в
состояние "2"; знак неравенства – к неравновесным.
В данной трактовке неравенства (2.1) существенно используется свойство
аддитивности функции энтропии: подразумевается, что S1 и
S2есть суммы энтропий, соответственно, исходных
веществ и конечных продуктов, взятых в пропорциях, определенных величинами
входящих и выходящих материальных потоков (балансовые уравнения будут выписаны
в Главе 3). Если речь идет об отдельном технологическом аппарате с единственным
входом и единственным выходом материального потока, то S1 и S2
есть просто энтропии выделенной массы рабочей смеси на входе и выходе аппарата.
Приложение неравенства (2.1) к анализу неравновесных процессов требует
однозначного истолкования интегрируемой величины 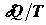 . Каждой элементарной порции
теплоты . Каждой элементарной порции
теплоты 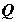 здесь
ставится в соответствие именно то значение Т, при котором система
воспринимает эту порцию теплоты (или отдает в окружающую среду). На рис. 2.1
изображена ситуация, когда в теплообмене системы с внешней средой участвуют три
отдельные части системы A, B и C, не находящиеся между
собой в тепловом равновесии. Тепловые потоки в эти подсистемы обозначены через здесь
ставится в соответствие именно то значение Т, при котором система
воспринимает эту порцию теплоты (или отдает в окружающую среду). На рис. 2.1
изображена ситуация, когда в теплообмене системы с внешней средой участвуют три
отдельные части системы A, B и C, не находящиеся между
собой в тепловом равновесии. Тепловые потоки в эти подсистемы обозначены через 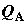 , , 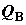 и и 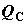 . В данном случае интеграл от
приведенной (нормированной по температуре) теплоты для целой системы
представляет собой сумму . В данном случае интеграл от
приведенной (нормированной по температуре) теплоты для целой системы
представляет собой сумму
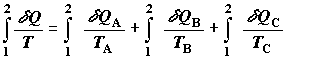 , ,
где TA, TB и TC – мгновенные
значения температур соответствующих подсистем. Если между внешней средой и
участвующей в теплообмене с ней частью системы поддерживается конечный перепад
температуры, то при расчете изменения энтропии в системе соответствующее
количество подведенной (отведенной) теплоты необходимо относить именно к температуре
системы. При этом изменение энтропии внешней среды в том же процессе будет
определятся уже температурой самой среды (см. по этому вопросу раздел 2.2.1).
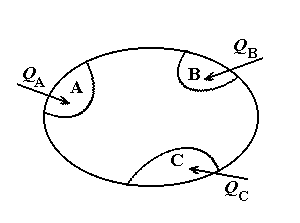
Рис.2.1. Теплообмен между внешней
средой и термически неоднородной системой.
Неравенство (2.1) показывает, что в гипотетическом равновесном процессе 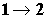 , идущем через
непрерывную последовательность промежуточных равновесных состояний
перерабатываемых веществ, изменение энтропии полностью определяется подводом
теплоты от внешнего источника (отводом теплоты во внешнюю среду). Функционирование
любой реальной технологической системы сопровождается самопроизвольными
неравновесными процессами внутри системы, т.е. действием внутренних источников
энтропии, помимо теплообмена с внешней средой. Поэтому при фиксированных
начальном и конечном состояниях перерабатываемого вещества, т.е. при
фиксированном результирующем изменении его энтропии, интеграл от приведенной
теплоты для любого неравновесного перехода , идущем через
непрерывную последовательность промежуточных равновесных состояний
перерабатываемых веществ, изменение энтропии полностью определяется подводом
теплоты от внешнего источника (отводом теплоты во внешнюю среду). Функционирование
любой реальной технологической системы сопровождается самопроизвольными
неравновесными процессами внутри системы, т.е. действием внутренних источников
энтропии, помимо теплообмена с внешней средой. Поэтому при фиксированных
начальном и конечном состояниях перерабатываемого вещества, т.е. при
фиксированном результирующем изменении его энтропии, интеграл от приведенной
теплоты для любого неравновесного перехода 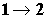 будет меньше, чем в равновесном процессе.
Разность будет меньше, чем в равновесном процессе.
Разность
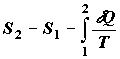
характеризует как раз действие внутренних источников энтропии в системе.
Таким образом, эквивалентной формой записи второго начала термодинамики будет
формулировка Пригожина
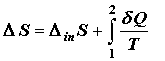 , (2.2) , (2.2)
где 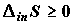 –
производство (генерирование) энтропии внутри системы. Было бы неаккуратно,
интерпретируя первое слагаемое правой части (2.2) как меру неравновесности
системы, отождествлять второе слагаемое с равновесной составляющей
результирующего изменения энтропии, поскольку обмен теплотой с окружающей
средой может протекать как квазиравновесно, так и в далеких от равновесия
условиях. Точнее говорить о внутрисистемной и межсистемной составляющих в
изменении энтропии. –
производство (генерирование) энтропии внутри системы. Было бы неаккуратно,
интерпретируя первое слагаемое правой части (2.2) как меру неравновесности
системы, отождествлять второе слагаемое с равновесной составляющей
результирующего изменения энтропии, поскольку обмен теплотой с окружающей
средой может протекать как квазиравновесно, так и в далеких от равновесия
условиях. Точнее говорить о внутрисистемной и межсистемной составляющих в
изменении энтропии.
Уже в исходных формулировках второго закона термодинамики содержится
указание на особое значение равновесных траекторий преобразования вещества с
точки зрения сопутствующего ему преобразования форм энергии. Поясним это на
простом примере изотермического процесса, знакомом читателю из курса физической
химии. Пусть в технологической установке (например, топливном электрохимическом
модуле) в процессе химического превращения веществ производится работа 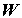 за счет убыли
внутренней энергии реагентов за счет убыли
внутренней энергии реагентов 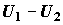 и подвода теплоты и подвода теплоты 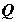 от внешнего теплоносителя: от внешнего теплоносителя:
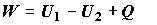 . (2.3) . (2.3)
В соответствии с (2.2) при условии Т= const
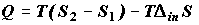 . (2.4) . (2.4)
Суммируя (2.3) и (2.4), имеем
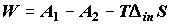 , (2.5) , (2.5)
где 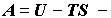 функция
Гельмгольца рабочих веществ. Выражения (2.4) и (2.5) показывают, что при
заданных начальном и конечном состояниях рабочего вещества (т.е. при заданных
изменениях функций состояния S и A чем более далеки условия
проведения процесса от равновесных и выше производство энтропии внутри системы,
тем меньшее количество теплоты система способна воспринять от внешнего
источника и тем меньшая часть изменения энергии Гельмгольца может превратиться
в работу. функция
Гельмгольца рабочих веществ. Выражения (2.4) и (2.5) показывают, что при
заданных начальном и конечном состояниях рабочего вещества (т.е. при заданных
изменениях функций состояния S и A чем более далеки условия
проведения процесса от равновесных и выше производство энтропии внутри системы,
тем меньшее количество теплоты система способна воспринять от внешнего
источника и тем меньшая часть изменения энергии Гельмгольца может превратиться
в работу.
Выражения (2.3) – (2.5) остаются справедливыми и для противоположно
направленного изотермического процесса (например, в электролизере), когда
системой потребляется работа 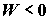 для осуществления химического превращения, характеризуемого
возрастанием энергии Гельмгольца реагентов. Чем выше производство энтропии в
системе, тем большее количество теплоты, в соответствии с уравнением (2.4),
потребуется отвести от системы, и тем выше будет, согласно (2.5), затрачиваемая
работа. для осуществления химического превращения, характеризуемого
возрастанием энергии Гельмгольца реагентов. Чем выше производство энтропии в
системе, тем большее количество теплоты, в соответствии с уравнением (2.4),
потребуется отвести от системы, и тем выше будет, согласно (2.5), затрачиваемая
работа.
Отметим, что в рассмотренном примере использовалась упрощенная форма записи
первого закона термодинамики (2.3), не учитывающая изменение механической
энергии рабочих веществ. Для общего анализа технологических систем, включающего
рассмотрение неизотермических процессов и принимающего во внимание изменение
механической энергии потоков, потребуется определенная модификация уравнений
первого и второго законов термодинамики, которая будет выполнена в Главах 3 и
4.
В химической технологии основными источниками генерации энтропии являются:
химические взаимопревращения компонентов; процессы, направленные на
выравнивание интенсивных параметров – температуры и химических потенциалов
компонентов по объему фаз, включая турбулентное смешение, теплопроводность и
молекулярную диффузию, тепловое излучение; диссипация механической энергии за
счет трения при перемещении рабочих веществ.
Торопливый читатель может далее сразу перейти к разделу 2.3, принимая как
данность центральное уравнение термодинамики неравновесных процессов для
скорости производства энтропии. В нижеследующем разделе 2.2 на классических
модельных примерах, ассоциирующихся с именами Пригожина (энтропия теплового
уравновешивания двух тел) и Вант-Гоффа (модель равновесного ввода в систему и
вывода из системы химического вещества через селективно проницаемую мембрану),
противопоставлены неравновесные и равновесные варианты необратимых по своей
природе процессов – теплового смешения, смешения веществ и превращения веществ.
Аккордное и, как представляется автору, нестандартное обсуждение модельных
неравновесных систем, которым отводится определенное место и в курсах
физической химии, имеет своей целью закрепление понимания студентом
закономерностей производства энтропии для каждого типа процессов и принципов
приближения к их равновесным траекториям. В традиционном курсе физической химии
закономерности производства энтропии неизбежно отодвигаются на второй план,
поскольку их приложение выходит за рамки этой учебной дисциплины. В теории
технологических процессов эти закономерности приобретают первостепенное значение;
задачей технолога является противодействие их проявлению. Хотя конкретные
способы такого противодействия технолог выбирает иные, чем манипулирование
цилиндрами с поршнями в модельных примерах.
|

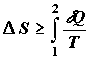 . (2.1)
. (2.1)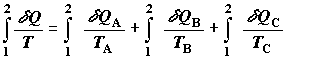 ,
,
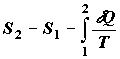
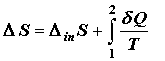 , (2.2)
, (2.2)