2.2.1. Установление теплового равновесия
Рассмотрим перенос теплоты при контакте двух тел, имеющих первоначально
различную температуру T10 и T20; 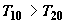 . Пусть массы
тел равны соответственно m1 и m2; удельные
теплоемкости c1 и c2, причем в исследуемом
интервале температур теплоемкости допустимо считать постоянными. В результате
переноса теплоты от нагретого к холодному телу их температуры выравниваются.
Равновесную температуру
. Пусть массы
тел равны соответственно m1 и m2; удельные
теплоемкости c1 и c2, причем в исследуемом
интервале температур теплоемкости допустимо считать постоянными. В результате
переноса теплоты от нагретого к холодному телу их температуры выравниваются.
Равновесную температуру 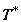 нетрудно рассчитать из энтальпийного баланса. Изменение
энтальпии первого тела составит
нетрудно рассчитать из энтальпийного баланса. Изменение
энтальпии первого тела составит 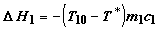 ; изменение энтальпии второго тела
; изменение энтальпии второго тела 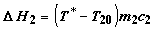 . Предполагая
отсутствие теплообмена с внешней средой, т.е. постоянство энтальпии системы в
целом, из равенства
. Предполагая
отсутствие теплообмена с внешней средой, т.е. постоянство энтальпии системы в
целом, из равенства 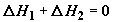 найдем
найдем
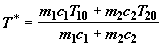 .
.
Каким образом рассчитать изменение энтропии в рассматриваемом
самопроизвольном процессе выравнивания температур двух тел? Для этого
необходимо мысленно произвести равновесное охлаждение первого тела от T10
до 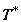 и
равновесное нагревание второго тела от T20 до
и
равновесное нагревание второго тела от T20 до 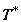 , определить интегралы от
приведенных теплот для этих двух процессов и, сложив их, найти суммарное
изменение энтропии системы. Достаточно поучительно рассмотреть два варианта
перехода от начального к конечному состоянию системы.
, определить интегралы от
приведенных теплот для этих двух процессов и, сложив их, найти суммарное
изменение энтропии системы. Достаточно поучительно рассмотреть два варианта
перехода от начального к конечному состоянию системы.
Первый вариант состоит в разъединении двух тел тонкой перегородкой, имеющей
значительно более низкую теплопроводность по сравнению с теплопроводностью
обоих тел. В таком случае скорость выравнивания температуры по объему каждого
из тел будет значительно выше, чем скорость изменения перепада температуры на
теплопередающей перегородке. Другими словами, при постепенном охлаждении
первого тела и нагревании второго тела распределение температуры в каждом из
тел будет сохраняться практически однородным (рис. 2.2), и с точки зрения
изменения термодинамического состояния каждого тела процесс будет протекать
квазиравновесно. Изменение энтропии в равновесном процессе охлаждения первого
тела составит
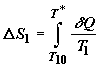 ,
,
где элементарная порция отводимой теплоты 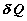 связана с изменением текущей температуры
телаT1 как
связана с изменением текущей температуры
телаT1 как 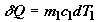 . Отсюда
. Отсюда
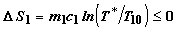 .
.
Аналогично изменение энтропии второго тела будет равно
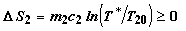 .
.
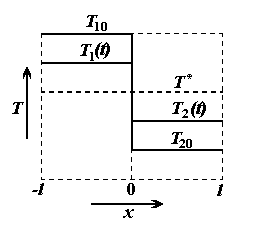
Рис. 2.2. Профили температуры в
начальный момент времени, в некоторый промежуточный момент времени 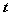 и при
установлении теплового равновесия в системе из двух тел, разделенных
перегородкой, слабо проводящей теплоту, для случая
и при
установлении теплового равновесия в системе из двух тел, разделенных
перегородкой, слабо проводящей теплоту, для случая 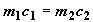 .
.
Изменение энтропии системы в целом в пренебрежении изменением энтропии тонкой
перегородки, имеющей бесконечно малую массу, составит
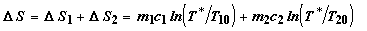 . (2.6)
. (2.6)
Поскольку данная система не участвует в теплообмене с внешней средой, весь
прирост энтропии связан здесь с необратимым переносом теплоты внутри системы,
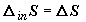 .
.
Как нетрудно убедиться, выражение (2.6) удовлетворяет условию 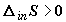 при
при 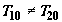 .
.
Выражение (2.6) характеризует также производство энтропии и при
непосредственном контакте тел (без разъединяющей их перегородки с низкой
теплопроводностью), так как начальные и конечные состояния тел совпадают.
Отличие двух систем состоит в том, что в системе без перегородки температурное
поле неоднородно по объему каждого из тел, и соответственно производство
энтропии распределено по всей системе, а в системе с перегородкой все
производство энтропии связано с переносом теплоты через тонкую перегородку,
т.е. как бы сосредоточенно на поверхности контакта тел.
Другой вариант перевода системы из начального в конечное состояние основан
исключительно на равновесных операциях. Разъединим тела и мысленно поместим
каждое из них в термостаты с регулируемым изменением температуры. В одном
термостате охлаждаем первое тело от T10 до 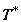 , а в другом термостате
нагреваем второе тело от T20 до
, а в другом термостате
нагреваем второе тело от T20 до 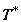 . Если скорость изменения
температуры в термостате поддерживается значительно ниже скорости выравнивания
температуры по объему тела, то теплообмен между термостатом и телом может
считаться квазиравновесным. Изменения энтропии двух тел
. Если скорость изменения
температуры в термостате поддерживается значительно ниже скорости выравнивания
температуры по объему тела, то теплообмен между термостатом и телом может
считаться квазиравновесным. Изменения энтропии двух тел 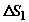 и
и 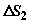 будут при этом в точности
совпадать с рассчитанными выше для системы со слабопроводящей перегородкой.
Суммарное изменение энтропии будет выражаться соответственно формулой (2.6).
Принципиальным отличием данного варианта является то, что все изменение
энтропии связано здесь с обратимым внешним теплообменом; генерация энтропии
отсутствует,
будут при этом в точности
совпадать с рассчитанными выше для системы со слабопроводящей перегородкой.
Суммарное изменение энтропии будет выражаться соответственно формулой (2.6).
Принципиальным отличием данного варианта является то, что все изменение
энтропии связано здесь с обратимым внешним теплообменом; генерация энтропии
отсутствует, 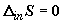 .
.
Механизм возникновения энтропии наиболее ясен при дифференциальном анализе
переноса теплоты между телами с разной температурой. В модели системы со
слабопроводящей перегородкой каждой элементарной порции теплоты 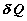 , переданной от первого
тела второму, соответствует изменение энтропии первого тела
, переданной от первого
тела второму, соответствует изменение энтропии первого тела 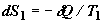 и изменение энтропии второго
тела
и изменение энтропии второго
тела 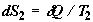 , где T1
и T2 текущие значения температуры тел. Отсюда суммарное
производство энтропии при переносе теплоты
, где T1
и T2 текущие значения температуры тел. Отсюда суммарное
производство энтропии при переносе теплоты 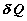 равно
равно
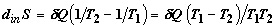 . (2.7)
. (2.7)