3.2. Уравнение баланса потоков энергии

Составим интегральное уравнение сохранения энергии в технологической системе, применимое к системам различного уровня сложности - как к целым производствам, так и к отдельным технологическим аппаратам (агрегатам), и охватывающее широкое многообразие технологических процессов. Это уравнение связывает между собой три категории трансформаций энергии: 1) изменение полной энергии выходящих из системы материальных потоков по отношению к полной энергии поступающих в систему потоков; 2) совершаемую системой (над системой) макроскопическую работу и 3) обмен тепловой энергией между рассматриваемой системой и ее окружением. Вывод проведем для наиболее простой ситуации, когда имеется единственный сырьевой поток и единственный продуктовый поток; затем обобщим результат на системы с произвольным числом входов и выходов. Пусть в стационарном режиме система перерабатывает поток рабочего вещества 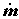. Скорость изменения полной энергии рабочего вещества при прохождении его через систему равна где_. , Дж/кг – удельная полная энергия вещества; и –значения удельной полной энергии на входе и на выходе из системы. Скорость подвода теплоты к системе обозначим как 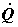,Дж/с и скорость совершения работы внутри системы, передаваемой внешнему потребителю, как 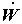, Дж/с. Наконец, учтем работу сил внешнего давления, которая затрачивается на прокачку жидкофазных или газофазных потоков через технологическую систему. Чтобы определить последнюю составляющую энергетического баланса, включим в контрольный объем, для которого составляется баланс, примыкающие к системе участки подводящего сырьевой поток и отводящего продуктовый поток трубопроводов (см. рис.3.2).

Пусть ( где j = 1, 2)обозначают соответственно площадь поперечного сечения трубопровода, среднюю линейную скорость перемещения рабочего вещества в трубопроводе, давление в трубопроводе и плотность рабочего вещества, причем j = 1 относится ко входу, а j = 2к выходу из системы. По законам механики силы внешнего давления на соответствующих границах контрольного объема (противоположно направленные) равны p₁A₁и p₂A₂, а скорость совершения работы силами внешнего давления в сумме

Рис. 3.2. К выводу уравнения баланса потоков энергии.

составит p₁-p₂. Произведения и представляют собой объемные расходы рабочего вещества (м³/с) на входе и выходе, причем и . Таким образом, скорость совершения работы силами внешнего давления (над рассматриваемой системой) выразится как .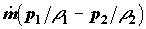

Просуммировав все потоки энергии, получаем уравнение сохранения энергии в технологической системе

.(3.6)

В этом уравнении 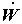считается положительной величиной, если работа передается внешнему потребителю, и , если система потребляет работу; напротив, , если теплота подводится к системе, и , если теплота отводится от системы.

Полную энергию рабочего вещества представим как сумму внутренней, кинетической и потенциальной (в поле силы земного притяжения) энергий. Тогда изменение удельной полной энергии запишется как

, (3.7)

где u_j – удельная внутренняя энергия; z_j – вертикальная координата соответственно для входа (j = 1) и выхода (j = 2); g–ускорение свободного падения. Вводя удельную энтальпию вещества , приведем уравнение (3.6) к окончательному виду

, (3.8)

где.

Замечание 1. Строго говоря, в уравнениях (3.7) и (3.8) слагаемые, характеризующие изменение кинетической энергии рабочего вещества, должны выражаться не через квадраты средней по поперечному сечению линейной скорости потока, а через средние по массовому расходу значения квадрата линейной скорости. Однако в большинстве случаев для потоков в подводящих и отводящих трубопроводах характерны большие значения критерия Рейнольдса, при которых основная масса рабочего вещества перемещается со скоростью, близкой к средней и поэтому

;

здесь – средняя по поперечному сечению скорость; – среднее по расходу рабочего вещества значение квадрата скорости; –линейная скорость как функция радиальной координаты,–R радиус трубопровода.

Замечание 2. Вывод уравнений баланса масс веществ и баланса различных форм энергии, как видит читатель, базируется здесь на понятии скорости подвода (отвода) массы вещества или конкретной формы энергии к системе. По сравнению с более традиционным способом составления уравнений баланса, основанным на подсчете количеств масс веществ или энергии, это сразу приводит к конечной форме уравнений баланса для стационарных процессов.

Слагаемые, характеризующие изменение кинетической и потенциальной энергии рабочего вещества, могут иметь важное значение при анализе механических процессов в отдельных технологических аппаратах; в энергетическом балансе химического производства в целом они обычно не учитываются:

. (3.9)

Уравнение (3.9) нетрудно обобщить на системы с произвольным числом входов и выходов:

, (3.10)

где h_j – удельная энтальпия материального потока через j-й вход (выход) системы. Как и при составлении материального баланса (см. предыдущий раздел), потоки считаются положительными для входов и отрицательными для выходов.

В левой части (3.10) стоит суммарное уменьшение энтальпии материальных потоков при их прохождении через систему. В силу закона сохранения масс химических элементов, выражаемого уравнением (3.2), потоки, выходящие из системы, в сумме составляют ту же самую смесь химических элементов, которую суммарно образуют потоки, входящие в систему. Поэтому для определения изменения энтальпии не возникает каких-либо препятствий, связанных с неопределенностью абсолютных значений энтальпии химических веществ. При любом выборе стандартных химических веществ, построенных из тех же самых химических элементов, которые входят в состав исследуемой системы, неопределенные константы при суммировании всех энтальпийных потоков взаимно сократятся.

Что включает в себя величина 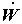при составлении общего энергетического баланса конкретного химического производства? Это может быть, например, работа рекуперативной газовой турбины или батареи топливных элементов, утилизирующих попутно получаемый водород, при условии, что эта работа не потребляется внутри самого производства, а передается внешнему потребителю (в виде электроэнергии). Аналогично в 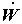входят, уже в виде отрицательных составляющих, расходы электроэнергии на работу насосов, компрессоров, мешалок, электропечей, электролизеров и т.д., входящих в состав производства и потребляющих электроэнергию из внешней сети.

Со своей стороны, применительно к балансу химического предприятия в целом, величина 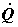может включать в себя отвод теплоты в системах внешнего водяного и воздушного охлаждения, либо напротив, нагревание охлажденных технологических потоков за счет теплообмена с окружающей воздушной или водной средой; сюда же входят потери тепловой энергии во внутрипроизводственных теплокоммуникациях и через стенки аппаратов. Таким образом, 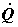обычно характеризует интенсивность теплообмена с окружающей природной средой. Что касается подводимых по трубопроводам от других промышленных объектов или поставляемых на смежные производства и в коммунальное хозяйство материальных потоков теплоносителей (в большинстве случаев это горячая вода или перегретый водяной пар), то они должны учитываться в левой части балансового уравнения (3.10). Здесь же учитывается энтальпия потоков отходов производства, включая сточные воды и дымовые газы.

Энергетический баланс технологической системы позволяет определить глубину происходящих процессов преобразования одних форм энергии в другие, а также обнаружить неконтролируемые потери энергии в окружающую среду.