Лекция 1. Поверхность потенциальной энергии химической реакции.
1.1 Поверхность потенциальной энергии (ППЭ)
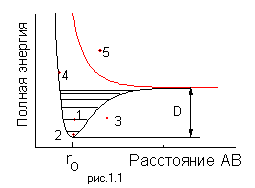
На Рис.1.1 показан связывающий и диссоциативный термы двухатомной молекулы AB. Энергия диссоциации молекулы составляет величину D. Конкретному состоянию двухатомной молекулы соответствует какая-либо изображающая точка на этом рисунке.
 |
Подробное рассмотрение таких термов читатель может найти в книгах по строению молекул и молекулярной спектроскопии. Отметим лишь, что информативность рисунка значительно возрастает, если считать, что по оси ординат отложена полная энергия системы. |
Рассмотрим теперь протекание простейшей
реакции обмена с участием молекулы AB:
АB + C A + BC (1)
 |
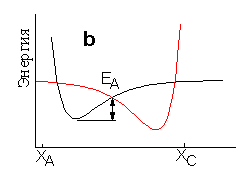 |
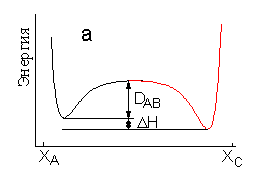
Пусть - это экзоэргическая реакция, т. е. реакция, протекающая с выделением энергии. Механизм такой реакции можно было бы представить себе как разрыв связи AB с образованием свободных атомов и затем образование связи BC. На Рис. 1.2а представлен идеализированный случай - атомы A и C закреплены на достаточно большом расстоянии в положении XA.и XC, а атом B изменяет свою координату. Протекание реакции в соответствии с таким механизмом не требует столкновения частиц - непосредственных участников реакции. Энергия активации такой реакции была бы равна энергии диссоциации разрывающейся связи т.е. составила бы величину порядка 200-400 кДж/моль. Если принять во внимание, что тепловая энергия при комнатной температуре составляет всего 2,4 кДж/моль на одну степень свободы, становится ясно, что такой механизм может реализоваться с заметной скоростью только при очень высоких температурах, и большинство химических реакций протекают другим образом. Для протекания большинства реакции необходимо столкновение реагирующих частиц. Схематически столкновению частиц соответствует Рис. 1.2b, на котором атомы A и C закреплены значительно ближе друг к другу. Если рассмотреть по отдельности термы молекулы AB и молекулы BC на этом рисунке, то видно, что энергия активации перехода атома B, которая определяется точкой пересечения термов, оказывается значительно меньше энергии диссоциации молекул. Однако рассмотрение близкорасположенных атомов A,B,C с помощью двухатомных термов не правомочно, поскольку наличие третьего атома, конечно, изменяет энергию связи двух других. Таким образом, диаграмма на Рис. 1.2b также неверно отражает протекание реального химического превращения.
Рассмотрим качественно, какова с позиции квантовой механики природа энергии активации в химической реакции, и чем определяется ее величина. Любая химическая реакция связана с перемещениями ядер атомов, из которых состоят молекулы реагентов, и с перестройкой их электронного окружения. Рассмотрение подавляющего большинства химических событий возможно на основе приближения Борна-Оппенгеймера, которое заключается в том, что вследствие малой массы электронов в сравнении с ядрами совокупность электронов в молекуле можно рассматривать как быструю подсистему. Это позволяет отдельно рассматривать и рассчитывать ядерное и электронное движения. Если ядра атомов находятся в некоторой конфигурации относительно друг друга, то электронное распределение приходит в соответствие с ядерной конфигурацией очень быстро, за время, за которое ядра практически не успевают переместиться. Быстрое электронная подсистема находится, таким образом, всегда в состоянии, которое определяется ядерной конфигурацией. Можно сказать, что электронное распределение отслеживает движения ядер и успевает подстроиться под них. С другой стороны, стационарное для данной ядерной конфигурации распределение электронной плотности определяет силы, действующие на ядра, и, таким образом, определяет их движение. Потенциальная энергия системы атомов определяется расположением электронов и ядер. Поскольку распределение электронов задано взаимным расположением ядер, то любому такому расположению соответствует единственное значение потенциальной энергии системы. Зависимость потенциальной энергии от ядерной конфигурации может быть выражена графически как поверхность потенциальной энергии (сокращенно ППЭ). Любой ядерной конфигурации будет соответствовать точка на поверхности потенциальной энергии. Для задания взаимного расположения ядер необходимо указать их координаты. Для молекулы, состоящей из N атомов, потребуется в общем случае 3N-6 координат, от каждой из которых зависит величина потенциальной энергии. Это означает, что потенциальная энергия системы из трех атомов зависит от трех координат и для своего пострения требует четырехмерного пространства. Таким образом, поверхность потенциальной энергии реальных химических систем является гиперповерхностью в многомерном пространстве.
Любой атом, как известно, может находиться в нескольких электронных состояниях (на различных электронных уровнях энергии). Нижнее по энергии электронное состояние устойчиво и называется основным, атомы в остальных электронных состояниях имеют большую энергию, поэтому эти электронные состояния называются возбужденными. Аналогичная ситуация характерна для систем атомов, т.е. молекул. Это означает, что молекула характеризуется не одной поверхностью потенциальной энергии, а системой таких поверхностей, одна из которых является основной, а остальные лежат выше по энергии и являются возбужденными. Эти поверхности потенциальной энергии соответствуют различным электронным состояниям системы - основному и возбужденным. Вообще говоря, их форма различна, и поэтому они могут пересекаться. Переход молекулы с одной поверхности потенциальной энергии на другую связан с изменением электронного и/или спинового состояния молекулы.
Если мы рассматриваем химическую реакцию, то две (или более) молекул, которые принимают в ней участие, находятся в сильном взаимодействии. Этот реакционный комплекс, так же как отдельная молекула, имеет свою систему поверхностей потенциальной энергии. Изменение положения ядер в ходе разрыва или образования химических связей представляет собой движение изображающей точки по поверхности потенциальной энергии. Если в ходе движения изображающая точка находится на одной поверхности потенциальной энергии, и влиянием (вероятностью заселения) других ППЭ можно пренебречь, то такую реакцию называют адиабатической. Это означает, что на протяжении всего процесса для описания системы можно пользоваться одной электронной волновой функцией.
1.2 Формула Лондона
Для определения вида поверхности потенциальной энергии и оценки величины потенциального барьера на пути реакции воспользуемся методом Лондона. Для этого рассмотрим реакцию (1) как систему трех атомов, каждый из которых имеет по одному валентному электрону. В квантовой механике состояние системы описывается соответствующей волновой функцией, которая является собственной функцией соответствующего оператора Гамильтона (гамильтониана):
![]() (1.1)
(1.1)
![]() (1.2)
(1.2)
где ![]() - оператор
кинетической энергии электронов, VeN, Vee,. VNN-потенциальная
энергия кулоновского взаимодействия электронов
с ядрами, межэлектронного отталкивания и
ядерного отталкивания, соответственно.
- оператор
кинетической энергии электронов, VeN, Vee,. VNN-потенциальная
энергия кулоновского взаимодействия электронов
с ядрами, межэлектронного отталкивания и
ядерного отталкивания, соответственно.
Пусть состояние исходных реагентов AB+C
описывается волновой функцией ![]() ab, а состояние
продуктов реакции A+BC -
ab, а состояние
продуктов реакции A+BC - ![]() bc. Эти функции в
одноэлектронном приближении и при пренебрежении
спин-орбитальным взаимодействием могут быть
построены из орбитальных функций a(x,y,z), b(x,y,z) и
c(x,y,z), которые описывают плотность распределения
валентного электрона вокруг изолированных
атомов A,B и C, и спиновых функций
bc. Эти функции в
одноэлектронном приближении и при пренебрежении
спин-орбитальным взаимодействием могут быть
построены из орбитальных функций a(x,y,z), b(x,y,z) и
c(x,y,z), которые описывают плотность распределения
валентного электрона вокруг изолированных
атомов A,B и C, и спиновых функций ![]() и
и ![]() , соответствующим
двум возможным спиновым состояниям электрона.
Каждая из функций
, соответствующим
двум возможным спиновым состояниям электрона.
Каждая из функций ![]() ab и
ab и ![]() bc будет состоять из
суммы произведений вида (a
bc будет состоять из
суммы произведений вида (a![]() )1(b
)1(b![]() )2(c
)2(c![]() ) 3. Индексы 1,2,3
обозначают номер электрона. Функции строятся
так, чтобы для устойчивой связи выполнялось
условие антисимметричности относительно
перестановки электронов, т.е. чтобы
удовлетворялся запрет Паули.
) 3. Индексы 1,2,3
обозначают номер электрона. Функции строятся
так, чтобы для устойчивой связи выполнялось
условие антисимметричности относительно
перестановки электронов, т.е. чтобы
удовлетворялся запрет Паули.
Нахождение энергии системы в промежуточном положении ядерных конфигураций между исходным и конечным состояниями системы, т.е. в области пересечения двухатомных термов производится вариационным методом. Суть метода заключается в рассмотрении интеграла:
![]() (1.3)
(1.3)
в который входят волновая функция изучаемой
системы ![]() , комплексно
сопряженная функция
, комплексно
сопряженная функция ![]() ,
гамильтониан H и энергия системы U.
Функция
,
гамильтониан H и энергия системы U.
Функция ![]() может быть
представлена в виде разложения по любому набору
функций:
может быть
представлена в виде разложения по любому набору
функций:
![]() (1.4)
(1.4)
Доказано, что если функция ![]() является собственной функцией, а U
является собственным значением гамильтониана H,
то интеграл J равен нулю. Таким образом,
формула (1.3) дает возможность, подставив
разложение (1.4), получить систему уравнений для
определения коэффициентов Ci. Эта схема
работает даже тогда, когда функции y i не
составляют полной и ортогональной системы. В
этом случае коэффициенты Ci и функция
является собственной функцией, а U
является собственным значением гамильтониана H,
то интеграл J равен нулю. Таким образом,
формула (1.3) дает возможность, подставив
разложение (1.4), получить систему уравнений для
определения коэффициентов Ci. Эта схема
работает даже тогда, когда функции y i не
составляют полной и ортогональной системы. В
этом случае коэффициенты Ci и функция ![]() , найденные для минимума
интеграла J, будут представлять собой
наилучшее приближение к собственной функции
гамильтониана.
, найденные для минимума
интеграла J, будут представлять собой
наилучшее приближение к собственной функции
гамильтониана.
В рассматриваемом случае будем искать
вариационную функцию ![]() в
виде разложения
в
виде разложения ![]() = C1
= C1
![]() ab
+ C2
ab
+ C2 ![]() bc .
bc .
Секулярные уравнения, получаемые из интеграла (1.3), выглядят следующим образом:
| C1 (HAA-SAAU)+ C2 (HAB-SABU)=0 C1 (HBA-SBAU)- C2 (HBB-SBBU)=0 |
(1.5) |
где:
| HAA = < HAB = HBA = < HBB = < SAA = < SAB = SBA = < SBB = < |
(1.6) |
Система уравнений (1.5) имеет ненулевое решение для коэффициентов разложения C1 и C2, только если ее детерминант равен нулю:
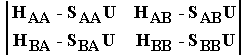 |
= 0 (1.7) |
Условие (1.7) позволяет найти собственные значения U как корни квадратного уравнения. Таким образом, задавая гамильтониан в виде (1.2), получим энергию системы атомов при любой заданной конфигурации ядер.
В ходе реализации этого метода необходимо рассчитывать интегралы (1.6). Так как
исходные волновые функции были построены из одноэлектронных функций a,b,c, то эти интегралы распадаются на алгебраические выражения из интегралов вида:
![]() ab=<a
ab=<a![]() b>,
b>, ![]() bc=<b
bc=<b![]() c>,
c>, ![]() ac=<a
ac=<a![]() c> (1.8)
c> (1.8)
Q=<(a)1(b) 2(c)3) ![]() He
He![]() (a)1(b)2(c)3)>
(1.9)
(a)1(b)2(c)3)>
(1.9)
(ab)= <(a)1(b) 2(c)3) ![]() He
He![]() (b)1(a) 2(c)3)>
(1.10)
(b)1(a) 2(c)3)>
(1.10)
(bca)= <(a)1(b) 2(c)3) ![]() He
He![]() (b)1(a) 2(c)3)>
(1.11)
(b)1(a) 2(c)3)>
(1.11)
Интегралы (1.8) получили название интегралов перекрывания. Интеграл (1.9) называется кулоновским интегралом, интегралы вида (1.10) - обменными интегралами, а интегралы виды (1.11) - интегралами двойного обмена.
Если считать, что исходные орбитали a,b,c ортогональны, то интегралы перекрывания равны нулю. Если, кроме того, пренебречь интегралами двойного обмена, то получится формула Лондона:
U![]() =Q
=Q![]() [1/2{[(ab)-(bc)]2+[(bc)-(ac)]2+[(ac)-(ab)]2}}1/2 (1.12)
[1/2{[(ab)-(bc)]2+[(bc)-(ac)]2+[(ac)-(ab)]2}}1/2 (1.12)
Если же не пренебрегать интегралами перекрывания (не считать исходные функции ортогональными), но удалить третий атом в бесконечность, то получится формула Гайтлера-Лондона для двухатомной молекулы с гомеополярной связью:
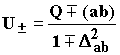 (1.13)
(1.13)
Эти формулы, полученные еще в двадцатые годы, оказались недостаточно точными даже для расчета молекулы водорода. Однако они объяснили природу химической связи и, в частности, возникновение потенциального барьера на пути реакции. Одним из главных вкладов здесь оказался обменный интеграл (совокупность обменных интегралов) или "обменное взаимодействие".
1.3 Поверхность потенциальной энергии в произвольных координатах
Рассмотрим вопрос, в каких координатах следует строить поверхность потенциальной энергии. Известно, что N атомов имеют в декартовом пространстве 3N координат. При объединении этих атомов в молекулу число независимых координат сохраняется. Так как три координаты из них будут характеризовать расположение и еще три координаты - ориентацию молекулы в пространстве, ясно, что внутренняя структура молекулы характеризуется 3N-6 (3N-5 для линейной молекулы) координатами. Исследователь имеет право выбрать эти координаты по своему усмотрению - это могут быть длины связей, углы и т.п. Рассчитывая для конкретных значений выбранных координат величины потенциальной энергии системы, можно получить поверхность потенциальной энергии. На рис. 1.3 показан результат одного из ранних расчетов поверхности потенциальной энергии для комплекса атома водорода с молекулой метана.
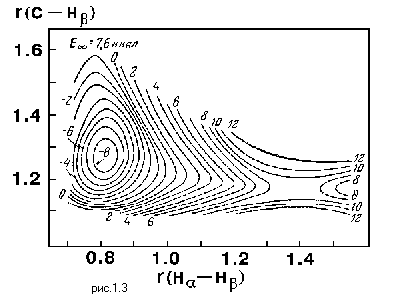
Обратим внимание на то, что рассматриваемая
система в реальности имеет много больше
внутренних степеней свободы, чем показано на
рисунке. Таким образом, исследователи, выбирая в
качестве координат расстояния H![]() -H
-H![]() и С-H
и С-H![]() , выбирают наиболее
интересное для них сечение многомерной
поверхности потенциальной энергии, а именно то,
которое наиболее наглядно иллюстрирует
изучаемый процесс. Недостаток построения
поверхности потенциальной энергии в произвольно
выбранных координатах заключатся в том, что
движение изображающей точки на такой
поверхности не подчиняется законам механики. Эта
точка не имеет постоянной массы, скорость ее
движения не характеризует кинетическую энергию
системы и т.д. Таким образом, наши интуитивные
механические представления о том, как должен
двигаться материальный шарик по такой
поверхности, могут привести исследователя к
неверным заключениям. В зависимости от выбора
координат вид поверхности потенциальной энергии
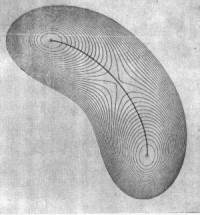
будет различным. На Рис.1.4 показана одна и та же
поверхность потенциальной энергии, построенная
при различном выборе координат. Поверхность
рассчитана для гипотетической молекулы,
претерпевающей изомеризацию A=B-C
, выбирают наиболее
интересное для них сечение многомерной
поверхности потенциальной энергии, а именно то,
которое наиболее наглядно иллюстрирует
изучаемый процесс. Недостаток построения
поверхности потенциальной энергии в произвольно
выбранных координатах заключатся в том, что
движение изображающей точки на такой
поверхности не подчиняется законам механики. Эта
точка не имеет постоянной массы, скорость ее
движения не характеризует кинетическую энергию
системы и т.д. Таким образом, наши интуитивные
механические представления о том, как должен
двигаться материальный шарик по такой
поверхности, могут привести исследователя к
неверным заключениям. В зависимости от выбора
координат вид поверхности потенциальной энергии
будет различным. На Рис.1.4 показана одна и та же
поверхность потенциальной энергии, построенная
при различном выборе координат. Поверхность
рассчитана для гипотетической молекулы,
претерпевающей изомеризацию A=B-C ![]() A-B=C:
A-B=C:
 |
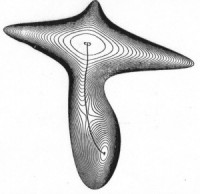 |
Рис. 1.4
Очевидно, что даже качественные выводы о вероятности движения изображающей точки по пути реакции оказываются совершенно ненадежными, поскольку глубина минимумов, высота перевалов на поверхности потенциальной энергии, также как форма поверхности зависят от выбора координат.
1.4 Поверхность потенциальной энергии в косоугольных координатах
Для того, чтобы движение изображающей точки по поверхности потенциальной энергии подчинялось законам механики, необходимо, чтобы кинетическая энергия этого движения выражалась стандартным образом:
![]() (1.14)
(1.14)
т.е. скорости ![]() должны
входить в выражение кинетической энергии в
квадрате, и в качестве коэффициента перед всеми
скоростями должна стоять одна и та же
эффективная масса.
должны
входить в выражение кинетической энергии в
квадрате, и в качестве коэффициента перед всеми
скоростями должна стоять одна и та же
эффективная масса.
Как уже показано выше поверхность потенциальной энергии, как правило, представляет собой гиперповерхность в многомерном пространстве, которую невозможно представить в наглядном виде. В связи с этим рассмотрим простейшую реакции обмена, протекающую при коллинеарном столкновении частиц:
АB + C![]() A + BC
A + BC
В этом случае потенциальная энергия зависит только от двух координат r1 и r2, и ППЭ может быть построена в трехмерном пространстве. Кинетическая энергия относительно центра масс всех трех частиц в координатах r1 и r2 выражается следующим образом:
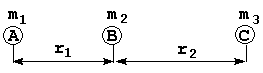
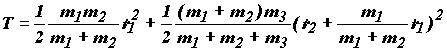
Раскрыв это выражение, получим
![]() (1.15)
(1.15)
где ![]()
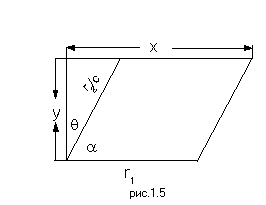
Для того, чтобы преобразовать это выражение к нужному виду (1.14), трансформируем систему координат так, как показано на Рис.1.5, т.е. изменим угол между координатами r1 и r2 и масштаб координаты r2 с коэффициентом С:
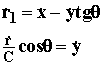 (1.16)
(1.16)
Тогда из равенства друг другу коэффициентов перед квадратичными членами в выражении (1.15) следует:
![]()
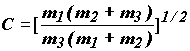 (1.17)
(1.17)
Угол ![]() определяется из условия
равенства нулю коэффициента перед перекрестным
членом. При подстановке (1.16) в (1.15) это условие
принимает вид:
определяется из условия
равенства нулю коэффициента перед перекрестным
членом. При подстановке (1.16) в (1.15) это условие
принимает вид:
![]()
Отсюда:
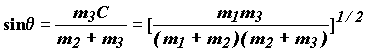 (1.18)
(1.18)
Кинетическая энергия системы в полученных новых координатах принимает вид:
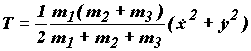 (1.19)
(1.19)
Пример поверхности потенциальной энергии, построенной в таких косоугольных координатах приведен на Рис.1.6.
Движение изображающей точки по этой
поверхности можно представить себе как движение
шарика с массой 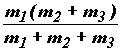 .
.
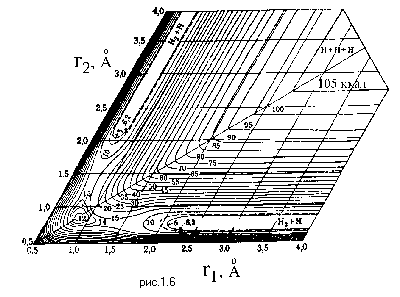
На поверхности потенциальной энергии можно выделить долину исходных реагентов и долину продуктов реакции, которые разделены переходной областью с более высокой потенциальной энергией. Линия, соединяющая долины исходных реагентов и продуктов реакции и отвечающая требованию минимальной потенциальной энергии, называется путем реакции, а длина, отложенная по этой линии - координатой реакции.
Качественный анализ такой поверхности
позволяет сделать важные заключения. Из формулы
(1.15) или из формулы для дополнительного угла ![]() :
:
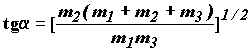 (1.20)
(1.20)
можно выяснить, насколько искривленным является путь реакции. Чем меньше угол между осями r1 и r2, тем больше вероятность отражения изображающей точки при попытке пройти из долины реагентов в долину продуктов. С другой стороны при малом угле ширина потенциального барьера, разделяющего долины реагентов и продуктов становится небольшой и возникает вероятность туннельного преодоления этого барьера вдали от области переходного состояния (седловины между долинами). Вероятность такого туннельного протекания реакции будет рассмотрена ниже.
Вероятность реакции определяется также шириной долины продуктов, т.е. шириной створа, в который должна попасть изображающая точка для протекания реакции. Относительная ширина створа долины исходных веществ и долины продуктов реакции определяется величиной масштабирующего коэффициента C, определенного формулой (1.17).
Если рассматриваемая система состоит более, чем из трех атомов, то нахождение аналогичных координат теряет смысл, так как соответствующая поверхность в пространстве более трех координат все равно не может быть изображена и не может быть использована для качественного визуального анализа. Численный же расчет движения системы может производиться в любых координатах. Однако во многих случаях возможен качественный анализ, при котором многоатомная система сводится к трехатомной. Примером может служить реакция:
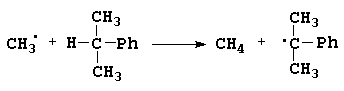
в которой также легко выделить разрываемую и образующуюся связи и выделить три фрагмента A,B и C.
1.5 Нормальные координаты
Для многих реакций рассмотрение поверхности потенциальной энергии в косоугольных координатах, основанное на аналогии с системой трех атомов, не применимо. В таких случаях задача выбора координат для поверхности потенциальной энергии производится на основе анализа нормальных колебаний. Главной целью при этом является определение тех движений атомов или их групп, которые представляют собой движение по координате реакции.
Пусть поверхность потенциальной энергии выражена функцией декартовых координат атомов. Разложим эту функцию в ряд Тейлора вблизи экстремума ППЭ (в стационарной точке):
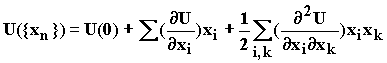 (1.21)
(1.21)
Принимая за точку отсчета потенциальной энергии ее величину в точке экстремума, с учетом равенства нулю первых производных в точках максимумов и минимумов функции имеем:
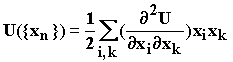
Перейдем к массовзвешенным координатам ![]() и обозначим
и обозначим
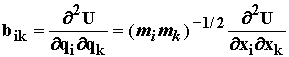
получим: 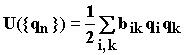 (1.22)
(1.22)
где ![]() представляет
собой силовые постоянные.
представляет
собой силовые постоянные.
Подставив теперь Лагранжиан:
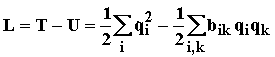 (1.23)
(1.23)
в уравнение движения
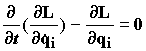
получим уравнения движения каждого атома:
![]() (1.24)
(1.24)
Видно, что в этой системе уравнений движение каждого атома, вообще говоря, зависит от координат остальных атомов. Однако известно, что линейным преобразованием координат, т.е. введением новых координат
![]() (1.25)
(1.25)
можно свести выражение (1.23) к квадратичной форме, а уравнение (1.24) к гармоническому виду:
![]()
имеющему решение:![]()
Поиск такого преобразования координат (т.е.
нахождение коэффициентов ![]() , с которыми входят в эти координаты
исходные координаты атомов) равносилен
диагонализации матрицы силовых постоянных. Для
многоатомных молекул эта задача сильно
упрощается, если принять во внимание элементы
симметрии молекулы. В координатах Qi движение
атомов в молекуле разбивается на 3N-6
гармонических независимых колебаний,
гармонических мод, в каждом из которых принимает
участие несколько атомов. Сами координаты Qi
имеют название нормальных координат, поскольку
движение по любой из этих координат не зависит от
движения по остальным нормальным координатам.
Подробное изложение методов
нормально-координатного анализа читатель может
найти в дополнительной литературе. Нам сейчас
важно, что если рассматривать молекулу,
находящуюся недалеко от дна потенциальной ямы,
или переходное состояние вблизи от вершины
барьера, то считая форму потенциальной
поверхности параболической, всегда можно найти
нормальные гармонические координаты.
, с которыми входят в эти координаты
исходные координаты атомов) равносилен
диагонализации матрицы силовых постоянных. Для
многоатомных молекул эта задача сильно
упрощается, если принять во внимание элементы
симметрии молекулы. В координатах Qi движение
атомов в молекуле разбивается на 3N-6
гармонических независимых колебаний,
гармонических мод, в каждом из которых принимает
участие несколько атомов. Сами координаты Qi
имеют название нормальных координат, поскольку
движение по любой из этих координат не зависит от
движения по остальным нормальным координатам.
Подробное изложение методов
нормально-координатного анализа читатель может
найти в дополнительной литературе. Нам сейчас
важно, что если рассматривать молекулу,
находящуюся недалеко от дна потенциальной ямы,
или переходное состояние вблизи от вершины
барьера, то считая форму потенциальной
поверхности параболической, всегда можно найти
нормальные гармонические координаты.
Симметрия молекулы накладывает свои ограничения как на вид электронных волновых функций, так и на типы и симметрию нормальных колебаний. Действительно, как электронная плотность в различных точках молекулы, так и энергия и частота колебаний, не должны меняться при действии элементов симметрии. В этом лежит причина того, что координате реакции соответствует одна из нормальных колебательных мод. Несмотря на то, что нормально координатный анализ применим только при небольших отклонениях системы от экстремумов потенциальной поверхности, обычно можно легко проследить, как нормальное колебание в переходном состоянии плавно переходит в одну из независимых степеней свободы (поступательную или колебательную) в долине исходных веществ и долине продуктов реакции. Очевидно, например, что реакция диссоциации молекулы воды протекает при возбуждении несимметричного валентного колебания:
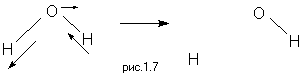
1.6 Задачи
1. Приведите примеры элементарных реакций различных типов, указанных в тексте.
2. Могут ли осуществиться ситуации, отмеченные на Рис.1.1 точками 1-5?. Каковы характеристики таких состояний и вероятность их реализации?
3. Определите, в каких случаях для описания химической реакции неприменимо адиабатическое приближение?. В каких случаях неприменимо приближение Борна-Оппенгеймера? Совпадают ли эти случаи? Приведите примеры.
4. Принцип Франка-Кондона, как известно, может быть сформулирован следующим образом: "Переходы между разными электронными состояниями (электронные переходы) происходят без изменения ядерных координат". Сформулируйте, как соотносится принцип Франка-Кондона с приближением Борна-Оппенгеймера и адиабатическим приближением.
5. Выберите координаты и представьте графически
качественный вид поверхностей потенциальной
энергии для:
а)реакции изомеризации цис-азометана в транс
изомер, протекающей по механизму вращения
метильной группы вокруг N=N связи (учтите
возможность диссоциации этой молекулы);
б)реакции образования димера уксусной кислоты в
газовой фазе;
в)реакции образования димера молекул R-Ph-Ph-CN в
газовой фазе;
г)реакции диссоциации радикала RO2. с учетом
возможности разрыва как C-O, так и O-O связей;
д)адсорбции молекулы азота на поверхности
металла;
е)адсорбции молекулы водорода на поверхности
металла;
ж)реакции RO2. + HR1 ![]() ROOH +.R1;
ROOH +.R1;
з)реакции распада ROOH.
Опишите характерные особенности полученных поверхностей.
6. Сравните поверхности потенциальной энергии для реакций:
RH + R1. ![]() R. + HR1
R. + HR1
HBr + Cl ![]() HCl + Br
HCl + Br
HBr + D ![]() DBr + H
DBr + H
Литература
Г.Эйринг, С.Г.Лин, С.М.Лин.
Основы химической кинетики. М.: Мир, 1983, 528 с.