|
Бутин К.П. Теоретическая стереохимия/ Органическая химия
Глава 8
Теоретическая стереохимия
8.1. Введение
Стереохимия изучает влияние пространственного
строения молекул на химические и
физико-химические свойства соединений.
Стереохимия - это "химия в пространстве"; она
имеет свой собственный подход к изучению
молекул, собственную теоретическую базу,
специальную терминологию для описания
стереохимических явлений, ее методы применимы ко
всем без исключения молекулярным объектам:
органическим, неорганическим,
металлоорганическим.
Под термином "пространственное строение"
подразумевают положение ядер составляющих
данную молекулу атомов в пространстве. Положение
же электронов (т.е. распределение электронной
плотности в молекуле) называют электронным
строением. Очевидно, что пространственное и
электронное строение молекулы тесно
взаимосвязаны: при изменении электронного
строения меняется положение ядер. Ярким примером
является рассмотренное в гл.2 резкое изменение
электронного строения метана при переходе этой
молекулы из обычной тетраэдрической в
"неприродную" плоскую форму. В стереохимии,
как правило, внимание концентрируется на
положении ядер, а электроны в явном виде
рассматриваются редко, т.е. обычно допускается,
что электроны оптимально (т.е. с наибольшим
связывающим эффектом) распределены в
пространстве вокруг ядер. Например, молекула NH3
имеет приблизительно тетраэдрическое
электронное строение (с учетом неподеленной
пары), но по положению ядер является тригональной
пирамидой (инвертирующейся). Подавляющее
большинство органических молекул имеет
трехмерную структуру, хотя известны и линейные
(одномерные), и плоские (двухмерные) молекулы.
Примером линейной молекулы является ацетилен,
примером плоской молекулы - бензол. В точном
смысле слова и ацетилен, и бензол трехмерные
молекулы, ибо они имеют "толщину", сравнимую
по величине с длиной (и шириной). Например,
диаметр молекулы бензола около 7 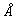 , а "толщина" около 3,5 , а "толщина" около 3,5 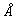 . "Толщина"
бензольного кольца обусловлена исключительно
размерами электронной оболочки, но его диаметр -
на 70% расстоянием между ядрами атомов. Ядерный
остов практически не имеет толщины, и поэтому,
если не учитывать электроны, молекулу бензола
можно считать плоской. . "Толщина"
бензольного кольца обусловлена исключительно
размерами электронной оболочки, но его диаметр -
на 70% расстоянием между ядрами атомов. Ядерный
остов практически не имеет толщины, и поэтому,
если не учитывать электроны, молекулу бензола
можно считать плоской.
В теоретической стереохимии атомы
рассматриваются как безразмерные точки, и
структура молекул описывается пространственной
группой таких точек, которые образуют
шестиугольник в случае бензола, прямую линию в
случае ацетилена, тетраэдр в случае метана и т.д.
Благодаря такому упрощению можно легко провести
классификацию молекул по топологии симметрии и
найти аналогию между, казалось бы, совершенно
разными структурами, например, между метаном и
адамантаном (см. раздел 8.2.2.г).
В трехмерном пространстве возникает явление,
которое называется стереоизомерия.
Стереоизомеры - это соединения, построенные из
одинакового набора атомов с одинаковой
последовательностью химических связей, но
отличающиеся расположением атомов в трехмерном
пространстве. Подобные изомеры для плоских
молекул, например, цис- и транс-изомеры
алкенов, обычно называют геометрическими
изомерами (гл.5).
Основными стереохимическими понятиями
являются хиральность, конфигурация и конформация,
смысл которых будет рассмотрен в следующих
разделах.
8.2. Оптическая активность и хиральность
Понятие о хиральных объектах (от греч. c e i r -
рука) было введено в конце XIX в. Кельвином.
Согласно определению, любая геометрическая
фигура или группа точек называется хиральной,
если отображение в идеальном плоском зеркале не
может быть совмещенным с нею самою. В химию
термин хиральность прочно вошел лишь в 1970-х
годах в результате теоретического изучения
оптически активных веществ. Явление оптической
активности известно с начала XIX в.; в его
изучение главный вклад внесли французские
ученые Д.Араго, Ж.Био, Л.Пастер, Э.Коттон,
О.Френель.
8.2.1. Оптическая активность
Оптическая активность - это способность среды
(кристаллов, растворов, паров вещества) вызывать
вращение плоскости поляризации проходящего
через нее оптического излучения (света).
Впервые оптическая активность была обнаружена
в 1811 г. Д.Араго в кристаллах кварца. В 1815 г. Ж.Био
открыл оптическую активность чистых жидкостей
(скипидара), а затем растворов и паров многих,
главным образом органических веществ. Ж.Био
установил, что поворот плоскости поляризации
происходит либо по часовой стрелке, либо против
нее, если посмотреть навстречу ходу лучей света и
в соответствии с этим разделил оптически
активные вещества на правовращающие
(вращающие положительно, т.е. по часовой стрелке)
и левовращающие (отрицательно вращающие)
разновидности. Наблюдаемое значение угла
поворота плоскости поляризации в случае
раствора связано с толщиной образца (l) и
концентрацией оптически активного вещества (С)
следующей формулой:
j = [a ] . l . С (8.1)
Коэффициент [a ] называется удельной оптической
активностью или удельным вращением.
Оптически активными веществами называют лишь
те вещества, которые проявляют естественную
оптическую активность. Существует также и
искусственная или наведенная оптическая
активность. Ее проявляют оптически неактивные
вещества при помещении в магнитное поле (эффект
Фарадея). Различить естественную или наведенную
оптическую активность довольно просто: если
линейно поляризованный свет (см. раздел 8.2.1.б),
прошедший через слой вещества с естественной
оптической активностью отражается и проходит
через вещество в обратном направлении, то
исходная поляризация света восстанавливается
(суммарный угол вращения j = 0). В среде же с
наведенной оптической активностью в аналогичном
опыте угол поворота удваивается. В дальнейшем мы
будем рассматривать лишь вещества с
естественной оптической активностью и для
краткости будем их называть просто "оптически
активными веществами".
8.2.1.а. Оптически активные вещества
Оптически активные вещества подразделяются на
два типа.
К первому типу относятся вещества, которые
оптически активны лишь в кристаллической фазе
(кварц, киноварь). Ко второму типу относятся
вещества, которые оптически активны в любом
агрегатном состоянии (например, сахара, камфора,
винная кислота). У соединений первого типа
оптическая активность является свойством
кристалла как целого, но сами молекулы или ионы,
составляющие кристалл, оптически неактивны.
Кристаллы оптически активных веществ всегда
существуют в двух формах - правой и левой; при
этом решетка правого кристалла зеркально
симметрична решетке левого кристалла и никакими
поворотами и перемещениями левый и правый
кристаллы не могут быть совмещены друг с другом.
Оптическая активность правой и левой форм
кристаллов имеет разные знаки и одинакова по
абсолютной величине (при одинаковых внешних
условиях). Правую и левую форму кристаллов
называют оптическими антиподами.
У соединений второго типа оптическая
активность обусловлена диссимметрическим
строением самих молекул. Если зеркальное
отображение молекулы никакими вращениями и
перемещениями не может быть наложено на
оригинал, молекула оптически активна; если такое
наложение осуществить удается, то молекула
оптически неактивна. (Под зеркалом понимают
отражатель, лежащий вне молекулы, и отражение
дает отображение всей молекулы). Следует особо
подчеркнуть, что необходимо употреблять
выражение "диcсимметрическое строение", а не
"асимметрическое строение".
Асимметрические молекулы не имеют никаких
элементов симметрии (кроме операции
идентичности; см.раздел 8.2.2.в), тогда как в
дисcимметрических молекулах некоторые элементы
симметрии остаются. Диcсимметрия есть нарушение
максимальной симметрии объекта.
Мы интуитивно чувствуем, что молекула
монозамещенного метана СН3Х должна
выглядеть "менее симметрично", чем молекула
незамещенного метана СН4, молекула
дизамещенного метана СН2ХY еще менее
симметрично, а молекула тризамещенного метана
СНXYZ (XN YN Z) еще менее симметрично. В этом ряду
возрастает степень диcсимметричности, но
полностью асимметричным можно назвать лишь
тризамещенный метан.
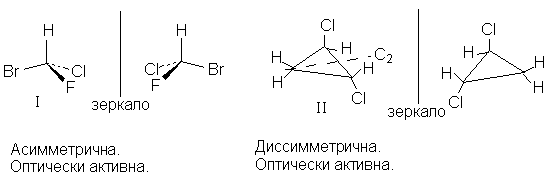
Молекула бромхлофторметана (I ) асимметрична, а
молекула транс-1,2-дихлорциклопропана (I I ) лишь
диcсимметрична, т.к. имеет ось симметрии второго
порядка (С2), но оба вещества оптически
активны, т.к. не идентичны своим зеркальным
отображениям.
Оптическую активность проявляют все
асимметрические молекулы, но далеко не все
диссимметрические молекулы. Так,
диcсимметрическая молекула
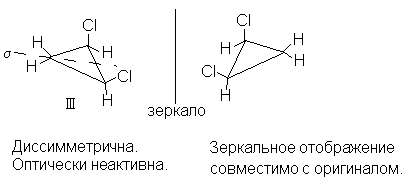
цис-1,2-дихлорциклопропана (I I I ), имеющая
плоскость симметрии s , проходящую через атом
углерода СН2-группы и середину связи С1-С2
перпендикулярно плоскости кольца (и поэтому не
асимметрическая), диссимметрична, но оптически
неактивна. Зеркальное отображение в этом случае
совместимо с оригиналом:
Следовательно, оптическая активность связана
лишь с определенным видом диcсимметрии (см.
раздел 8.2.2), а именно с дисcимметрией,
обусловливающей несовместимость объекта с его
зеркальным отображением. Такой же вид
диссимметрии, как сказано выше, получил название
хиральность. Хиральные объекты относятся друг к
другу как правая и левая рука, или винты с правой
и левой резьбой, т.е. они несовместимы в
пространстве и представляются как зеркальные
отображения друг друга. Оптически активная
молекула хиральна, а оптически неактивная ахиральна,
однако если молекулу нельзя совместить с ее
зеркальным отображением, то зеркальное
отображение соответствует другой, отличной
молекуле, которую, в принципе, можно
синтезировать. Синтезированное зеркальное
отображение хиральной молекулы будет ее
реальным оптическим изомером (не
рекомендуется употреблять термин оптический
антипод, как в случае кристаллов). Чистое
оптически активное соединение имеет два и только
два оптических изомера (т.к. каждому объекту
соответствует лишь одно зеркальное отображение).
Оптические изомеры называются энантиомерами
(или иногда энантиоморфами). Удельное вращение ([a
] в формуле (1)) энантиомеров одинаково по
абсолютной величине и противоположно по знаку:
один энантиомер левовращающий, а второй
правовращающий. Кроме знака вращения все другие
физические и химические свойства энантиомеров в
газовой фазе, а также в ахиральных жидких средах
одинаковы. Однако, если жидкая среда хиральна
(например, в раствор добавлен хиральный реагент
или катализатор, или сам растворитель хирален)
свойства энантиомеров начинают различаться. При
взаимодействии с другими хиральными
соединениями, отзывающимися на зеркальную
изомерию молекул, энантиомеры реагируют с
различными скоростями. Особенно ощутимо
различие в физиологическом и биохимическом
действии энантиомеров, что связано с
энантиомерией биологических реагентов и
катализаторов. Так, природные белки состоят из
левых оптических изомеров аминокислот и поэтому
искусственно синтезированные правые
аминокислоты организмом не усваиваются; дрожжи
сбраживают лишь правые изомеры сахаров, не
затрагивая левые и т.д.
Общее правило состоит в том, что энантиомеры
проявляют идентичные свойства в симметричном
(ахиральном) окружении, а в несимметричном
(хиральном) окружении их свойства могут
изменяться, Это свойство используется в
асимметрическом синтезе и катализе (см. раздел
8.6).
Смесь равных количеств энантиомеров, хотя и
состоит из хиральных молекул, оптически
неактивна, т.к. одинаковое по величине и
противоположное по знаку вращение взаимно
компенсируется. Такие смеси называют
рацемическими смесями или рацематами. В
газообразном состоянии, жидкой фазе и в
растворах свойства рацематов обычно совпадают
со свойствами чистых энантиомеров, однако в
твердом состоянии такие свойства, как
температура плавления, теплота плавления,
растворимость, обычно отличаются. Например,
рацемическая винная кислота плавится при 204-206° С,
а (+) или (-) -энантиомеры при 170° С. Растворимость
рацемической винной кислоты в воде в 6,7 раз ниже,
чем растворимость чистых энантиомеров.
8.2.1.б. Физические причины оптической
активности
В ахиральной среде два энантиомера имеют
одинаковые химические и физические свойства, но
их легко отличить друг от друга по
специфическому взаимодействию со светом. Один из
энантиомеров вращает плоскость поляризации
линейнополяризованного (плоскополяризованного)
света вправо, а другой энантиомер - на точно такой
же угол влево. Возникает вопрос: почему только
хиральные молекулы вращают плоскость
поляризации?
Феноменологическую модель оптической
активности предложил Френель еще в 1823 г. Она
основана на волновой теории света и с позиций
современной науки не является достаточно
строгой. Тем не менее эта модель дает очень
наглядное представление о причинах оптической
активности и других явлениях, связанных с
поглощением света хиральным веществом, в рамках
классической электродинамики, поэтому ее часто
используют и в настоящее время.
Согласно классическим представлениям,
линейнополяризованный (плоскополяризованный)
свет характеризуется тем, что векторы
составляющих его зависимых от времени
электрического (Е) и магнитного (Н) полей
осциллируют во взаимно перпендикулярных
плоскостях и их изменения носят синусоидальный
характер во времени и в пространстве (рис. 8.1.а).
Плоскополяризованный свет можно рассматривать
как комбинацию левого и правого
циркулярнополяризованных лучей, движущихся в
фазе по отношению друг к другу. На рис. 8.1.б-г
магнитные составляющие не показаны, а показаны
лишь электрические векторы в моменты времени
1,2,3,4 и 5. (Этого вполне достаточно т.к. магнитные
векторы всегда ориентированы ортогонально
электрическим). Если в начальной точке времени 1
электрические векторы левого и правого
циркулярнополяризованных лучей ориентированы
вверх, то в точке 2 вектор правого луча
ориентирован вправо, а вектор левого луча влево
(если смотреть в направлении движения света по
оси z). В точке 3 векторы обоих лучей ориентированы
вниз, в точке 4 вектор правого луча ориентирован
влево, а вектор левого луча вправо, и т.д. Таким
образом, правый и левый
циркулярнополяризованные лучи обладают
соответственно правой и левой спиральностью
вращения вектора электрического поля. Сумма этих
лучей дает плоскополяризованный луч (рис. 8.1.г),
причем в пространственно-временных точках 1,3 и 5
векторы суммируются, а в точках 2 и 4 взаимно
уничтожаются. Расстояние между точками 1 и 5
соответствует одному витку правой или левой
спирали или длине плоской волны (рис.8.1.г).
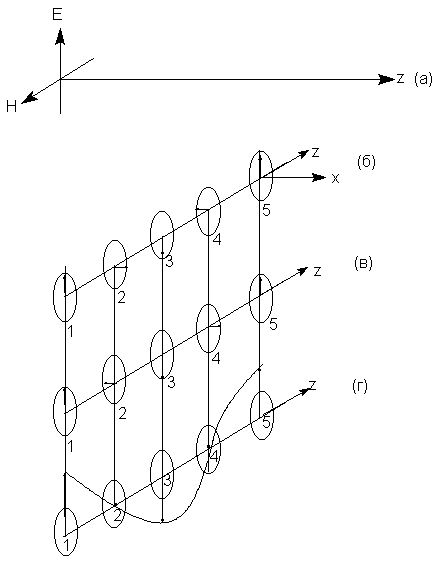 Рис. 8.1. Плоско (линейно) поляризованный
световой луч (а), правый (б) и левый (в)
циркулярно-поляризованные лучи (показаны только
векторы электрического поля). (г) - Результат
взаимодействия электрических векторов лучей (б)
и (в), находящихся в фазе.
При попадании света на любую молекулу в
прозрачной среде, скорость его замедляется
(уменьшение скорости пропорционально показателю
преломления среды), так как свет взаимодействует
с электронными оболочками молекул. Степень
такого взаимодействия зависит от поляризуемости
молекулы.
Если среда ахиральна, две
циркулярнополяризованные составляющие проходят
с одинаковой скоростью (т.е. с одинаковыми
показателями преломления для правого и левого
лучей). Однако хиральные молекулы проявляют
анизотропию поляризуемости, которая зависит от
того, левую или правую спиральность имеет
циркулярнополяризованный луч. Например, левый
циркулярнополяризованный луч может замедлиться
сильнее правого, тогда произойдет сдвиг по фазе.
Так как левый луч отстает от правого, векторы
равной амплитуды не будут находиться в
одинаковых фазах. В результате плоскость
прошедшего через хиральный раствор луча будет
вращаться на некоторый угол относительно
плоскости падающего луча (рис. 8.2.а). При
прохождении через хиральную среду в общем случае
неодинаковы не только скорости, но и
коэффициенты поглощения левого и правого
циркулярнополяризованных компонент
плоскополяризованного света. В результате
векторы для правого и левого прошедшего через
образец лучей будут иметь разную амплитуду, а
результирующий вектор будет описывать
эллиптическую траекторию (рис. 8.2.б). В общем, при
прохождении плоскополяризованного света через
хиральную среду вектор электрического поля
начинает описывать эллипс (эллиптическая
поляризация) с повернутой главной осью (рис. 8.2.в).
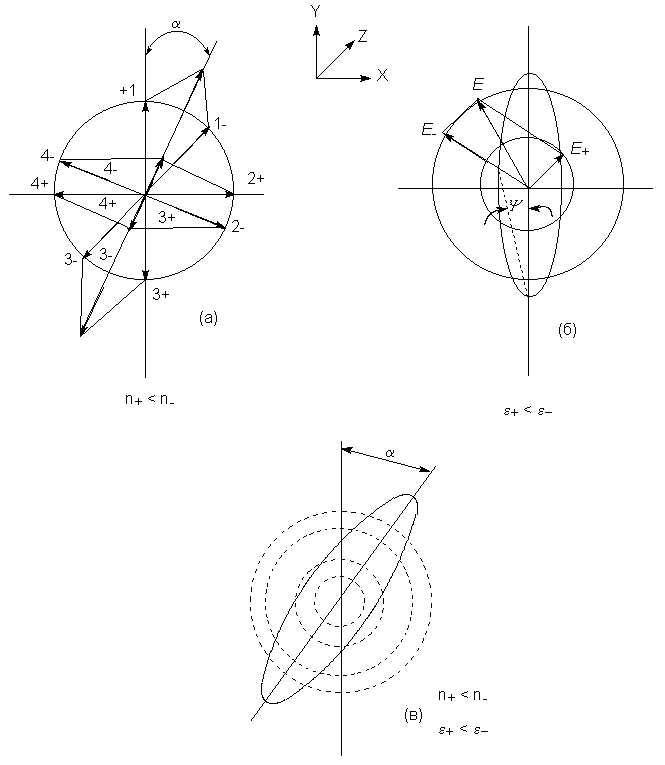
Полученное Френелем выражение для угла
поворота плоскости поляризации имеет вид:
a = p (l/l )(n+ + n-) (8.2)
где l - длина кюветы, l - длина волны света, n+
и n- - показатели преломления правого и
левого циркулярно-поляризованного компонента.
Как видно, угол вращения уменьшается с
увеличением длины волны падающего света. Однако
это справедливо лишь для света, длина волны
которого больше длины волны максимума
поглощения в электронном спектре данного
вещества. Изменение оптического вращения при
изменении длины волны называется дисперсией
оптического вращения (ДОВ).
Разность поглощения правой и левой компонент
называется круговым дихроизмом (КД).
Количественной характеристикой КД служит угол
эллиптичности y (рис. 2), величина которого обратно
пропорциональна длине волны
f = p (l/l )(e + - e -)
где e + и e - - коэффициенты
экстинкции. КД открыт Э. Коттоном в 1911 г. и его
часто называют эффектом Коттона. ДОВ и КД вместе
называются хирооптическими явлениями; в
своей основе они связаны с электронными
переходами в хиральном окружении. Эффект
Коттона, т.е. превращение плоскополяризованного
света в эллиптически поляризованный заметно
проявляется главным образом вблизи полос
собственного (резонансного) поглощения вещества.
Квантовую теорию оптической активности
построил в 1928 г. бельгийский физик Л. Розенфельд.
С позиций современной науки эта теория
рассматривается как более строгая. Для
объяснения оптической активности оказалось
необходимым учитывать взаимодействие
электрических и магнитных дипольных моментов,
наведенных в молекуле полем проходящей световой
волны.
В настоящее время возрождается интерес к
корпускулярной теории света. которой
придерживался еще Ньютон. Частицей света
является фотон - реальная элементарная частица. В
фотонной теории поляризацию света связывают с
поляризацией фотонов, которая обусловлена
наличием у этих частиц спина и его определенной
направленностью в пространстве. Спиновые
квантовые числа - это как бы дополнительные
внутренние степени свободы частицы. В отличие от
электронов, имеющих спин J = 1/2, спин фотона J = 1.
(Это означает, что электроны принадлежат к классу
фермионов, для которых справедлив запрет Паули, а
фотоны - к классу бозонов, для которых не
действует принцип запрета). Согласно квантовой
механике, частица со спином J и ненулевой массой
покоя имеет (2J + 1) внутренних квантовых состояний,
определяющих ее поляризацию, т.е. степень
асимметрии частицы в пространстве. Но масса
покоя фотона равна нулю, и поэтому число спиновых
состояний на единицу меньше, т.е. равно двум (+1 и
-1). Это означает, что возможны лишь две ориентации
проекции спина фотона на направление его
движения: параллельная и антипараллельная. В
таком случае возникает понятие "спиральность
частицы". Если проекция спина на направление
движения положительна, то говорят, что частица
имеет правовинтовую (правую) спиральность, а если
отрицательна - левовинтовую (левую) спиральность.
Спиральные объекты хиральны, поэтому фотоны
являются как бы хиральными частицами.
Поскольку фотоны обладают целочисленным
спином, в одном и том же состоянии может
находится любое число фотонов. Это обусловливает
возможность описания электромагнитных
взаимодействий с участием большого числа
фотонов в рамках классической (а не только
квантовой) механики. Циркулярно-поляризованный
свет можно рассматривать как поток фотонов,
имеющих только правую или только левую
спиральность. Плоскополяризованный свет состоит
из одинакового количества "левых" и
"правых" фотонов. Взаимодействие по-разному
поляризованных фотонов с хиральной анизотропной
средой происходит неодинаково, что приводит к
хироптическим эффектам.
Следует подчеркнуть, что ахиральная молекула
не вращает плоскость поляризации света только
при определенной ее ориентации по отношению к
падающему лучу. Например, ахиральная молекула,
имеющая плоскость симметрии, не вращает
плоскость поляризации лишь в том случае, если
плоскость поляризации совпадает с плоскостью
симметрии. Все же остальные молекулы, не
ориентированные таким образом, вращают
плоскость поляризации, даже не будучи
хиральными. Однако в целом образец не вращает,
так как в массе молекулы ориентированы
беспорядочно, и одни молекулы вращают плоскость
поляризации в одном направлении, а другие
молекулы, встречающиеся на пути светового луча,
вращают ее в противоположную сторону. Таким
образом коллектив ахиральных молекул имеет
суммарное вращение, равное нулю, хотя каждая
молекула может вращать плоскость поляризации. В
случае хиральных соединений молекул
противоположной ориентации (если это не
рацемическая смесь) просто не может
существовать, и вращение наблюдается.
8.2.1.в. Зависимость угла вращения от
условий измерения
Согласно уравнениям (8.1) и (8.2) для каждого
данного энантиомера величина вращения a зависит
от толщины образца, концентрации и длины волны
света. Кроме этих факторов a зависит от
температуры, давления (в случае газов) и природы
растворителя. Поэтому вместе с удельным
вращением указывают температуру и длину волны. ([a
]tl ). Обозначение [a ]D означает, что
вращение измерено при длине волны,
соответствующей D-линии натриевой лампы, т.е. при
589 нм (желтый свет). Часто используют величину
молярного вращения [М]tl . которая равна
удельному вращению [a ]tl , умноженному на
молекулярный вес и деленному на 100.
Известны случаи обращени знака вращения при
изменении длины волны, растворителя и
концентрации. Теоретически удельное вращение не
должно зависеть от концентрации, т.к.
концентрация уже учитывается в уравнении (8.1). Тем
не менее возможны отклонения от линейной
зависимости [a ] от С за счет ассоциации,
диссоциации и взаимодействия между
растворителем и растворенным веществом.
Например, хиральные карбоновые кислоты могут
менять знак и величину вращения в зависимости от
рН и основности растворителя, поскольку
недиссоциированная кислота и ее анион обладают
разным вращением.
Кривые ДОВ и КД тесно связаны с электронными
спектрами хиральных молекул (рис.8.3). В случае
индивидуального электронного перехода
максимумы на УФ- и КД-кривых и точка, в которой
кривая ДОВ меняет знак, почти совпадают. Пример
на рис.8.3 отвечает положительному эффекту
Коттона. Если же максимум на кривой КД и
длинноволновой экстремум кривой ДОВ
отрицательны (направлены вниз), то эффект Коттона
называется отрицательным. Энантиомеры дают
зеркально-симметричные кривые ДОВ и КД.
Если имеется несколько максимумов в УФ-спектре,
эффект Коттона может быть довольно сложным.
Хироптические методы щироко используются для
установления относительных конфигураций
молекул (см. раздел 8.4).
8.2.2. Хиральные молекулы
Теперь необходимо рассмотреть вопрос: как
определить, будет ли данная молекула хиральна?
Обязательным условием хиральности является
несовместимость объекта с зеркальным
отображением:
В случае простых молекул легко проводится
зрительное распознавание несовместимости с
зеркальным отображением. Однако многие
органические молекулы настолько сложны, что
такой способ требует очень развитого
пространственного воображения, которым обладают
далеко не все.
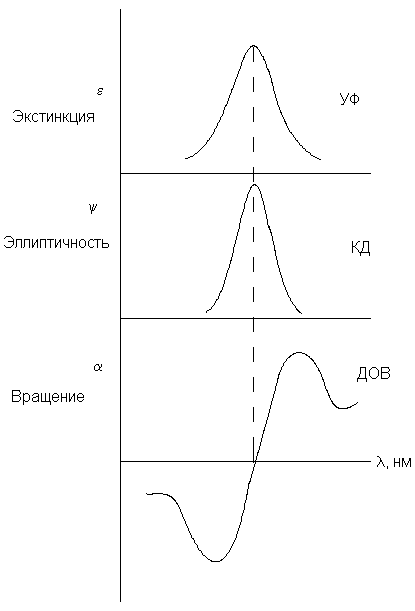
Рис.3. Соотношение между УФ-спектром, КД и ДОВ (в
случае индивидуальной полосы УФ-поглощения).
Следовательно, необходимо установить какие-то
общие критерии, облегчающие распознавание
хиральных молекул. Прежде всего обратимся к
теории симметрии и кратко рассмотрим элементы,
операции и группы симметрии.
8.2.2.а. Точечные группы симметрии
Шар самый симметричный объект, поскольку как бы
мы его не повернули, не переместили в
пространстве, не отразили в зеркале, он всегда
выглядит одинаково. Тетраэдр "менее
симметричен", чем шар, поскольку вокруг высоты
его нужно повернуть лишь на определенный угол (1200),
чтобы он выглядел так же, как до поворота.
Вращение вокруг оси является одной из операций
симметрии. Операцией симметрии называется
действие над объектом, которое приводит к его
новой ориентации, неотличимой от исходной и
совмещаемой с нею.
Операции симметрии, которые мы будем
рассматривать, таковы, что по крайней мере одна
точка объекта остается неподвижной. Такие
операции симметрии называются точечными, а
неподвижная точка, которая не меняет положения
при всех точечных операциях симметрии этого
объекта - это центр тяжести объекта, в котором
пересекаются все оси и плоскости симметрии.
Такой точкой являются центры шара или тетраэдра.
Каждой операции симметрии соответствует
определенный элемент симметрии. Элементом
симметрии называется геометрическое место
точек, остающихся неподвижными при данной
операции симметрии. Основными элементами
симметрии являются собственные оси вращения,
которые в системе обозначений Шенфлиса имеют
символ Cn, где n - порядок оси, означающий, что
поворот молекулы на угол 2p /n радиан приводит к
структуре, неотличимой от первоначальной, несобственные
оси вращения или зеркально-поворотные оси (s n),
зеркальные плоскости симметрии (s ), делящие
молекулу пополам, так, что одна половина является
зеркально-симметричной другой половине, центр
инверсии (i) и тождественное преобразование
(Е). В сответствии с этим операции симметрии делят
на поворот оси вокруг оси симметрии Сn,
поворот вокруг оси с последующим отражением в
плоскости, перпендикулярной этой оси (Sn),
отражение в плоскости симметрии s , инверсию в
центре симметрии i и операцию идентичности Е. При
операции идентичности с молекулой ничего не
делают, но эта операция не бессмыслена, т.к. она
позволяет включить в единую классификацию как
симметричные, так и асимметричные объекты.
Рассмотрим несколько подробнее два главных
вида элементов симметрии и связанные с ними
операции симметрии: собственную и несобственную
оси вращения.
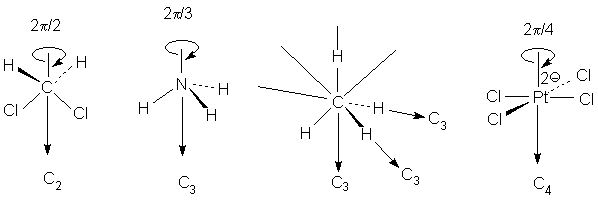
Собственная ось симметрии. Все молекулы
имеют тривиальную ось С1, поскольку в любом
случае вращение на 3600 возвращает молекулу
в исходное состояние. Следовательно, операция С1
эквивалентна операции идентичности (С1 є Е).
Дихлорметан имеет ось С2, аммиак - ось С3,
метан - четыре оси С3, тетрахлорплатинат -
ось С4.
Несобственная ось симметрии. Простейшая
зеркально поворотная ось S1 эквивалентна
перпендикулярной ей плоскости симметрии (S1
є s ). Примером является молекула хлорфторметана.
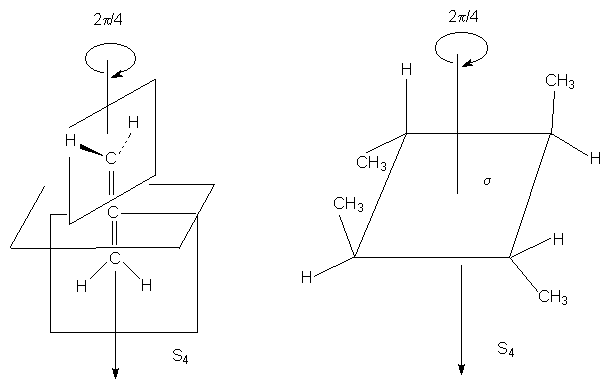
Зеркально-поворотные оси более высокого порядка
(Sn) можно рассматривать как комбинацию
вращения на угол 2p /n с последующим отражением в
плоскости, перпендикулярной оси вращения. Так,
аллен и изображенный ниже изомер
1,2,3,4-тетраметилциклобутана имеет
зеркально-поворотную ось S4:
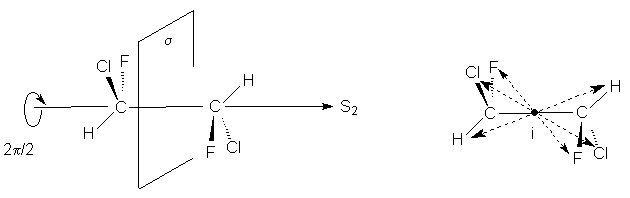
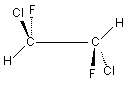
1,2-Дихлор-1,2-дифторэтан обладает осью S2,
которая совпадает со связью С-С. Как видно
операция S2 эквивалентна инверсии в центр
симметрии, который в данном случае находится
посредине связи С-С (S2 є i)
Точечные группы симметрии. Поскольку у
молекул может быть не один, а несколько элементов
симметрии, их удобнее классифицировать по
точечной группе симметрии. Набор все операций
симметрии объекта образует его группу симметрии.
Если при всех этих преобразованиях остается
неподвижным центр тяжести фигуры, то группа
симметрии называется точечной. Известны четыре
типа точечных групп симметрии, которые
представлены в табл. 8.1.
Таблица 8.1
Точечные группы симметрии
Тип |
Обозначение |
Элементы симметрии |
Примеры |
| 1 |
С1 |
E є C1 |
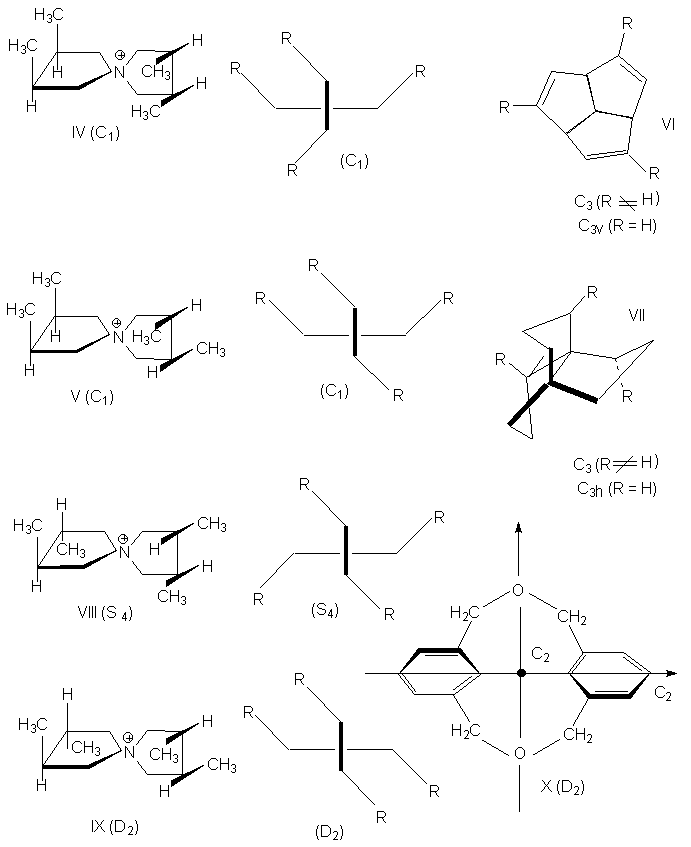
Соединения IV и V |
| |
CS |
S1 є s |
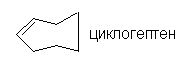 |
| |
Ci |
S2 є i |
 |
| 2 |
Cn |
Cn |
Соединения VI и VII при R N H (C3) |
| |
Sn |
Sn + Cn/2 |
Соединение VIII (S4) |
| |
Сnv |
Sn + ns v |
H2O (C2v), NH3 (C3v),
конус (СҐ v), циклогексан (С3v) |
| |
|
|
Соединение VI при R = H (С3v) |
| |
Сnh |
Cn + 1s h |
Соединение VII при R = H |
| 3 |
Dn |
Cn + nC2^ Cn |
Соединения IX и X (D2) |
| |
Dnd |
Cn + nC2^ Cn + ns v |
|
| |
Dnh |
Cn + nC2^ Cn + ns v
+ s n |
Бензол (D6h);
1,3,5-трихлор-бензол (D3h) |
| |
|
|
Цилиндр (DҐ h) |
| 4 |
Td |
4C3 + 3C2 + 6S4 + 6s |
Тетраэдр (метан, адамантан) |
| |
Oh |
3C4+ 4C3 +6C2 + i + 9s |
Октаэдр |
| |
Ih |
|
Икосаэдр, додекаэдр |
К типу 1 относятся точечные группы С1, Сs,
Ci, которые не имеют нетривиальных
поворотных осей, поэтому их называют
неаксиальными. К типу 2 относятся группы с
единственной поворотной осью. В группе Cn
других элементов симметрии нет, в группе Cnv
имеется n вертикальных плоскостей s n,
проходящих через ось Cn, а в группе Сnh
одна горизонтальная плоскость s h,
перпендикулярная оси Сn. Сюда же входит
группа Sn, поскольку при наличии
зеркально-поворотной оси порядка n обязательно
имеется и собственная ось порядка n/2 (C2 у S4,
C3 у S6 и т.д.). При нечетном n оси Sn
могут быть представлены как комбинации других
операций. Для низших порядков S1 є s и S2
є i. Точечные группы типа 3 имеют одну ось Сn
и n осей второго порядка, перпендикулярных оси Сn.
Такие группы называются диэдральными. Если нет
плоскостей симметрии, группа обозначается как Dn,
если имеется несколько плоскостей s v
(вертикальных) - Dnd, а если еще и
горизонтальная плоскость s h, то группа
обозначается Dnh. К типу 4 относятся точечные
группы, имеющие более чем одну ось порядка выше
двух. Такие группы называются кубическими. К ним
относятся точечные группы правильных тетраэдра
(Td), октаэдра и куба (Oh), икосаэдра и
додекаэдра (Ih). Максимальную симметрию
имеет шар, который принадлежит предельной группе
Kh, включающей все возможные операции
симметрии.
Отметим, что термины "тетраэдрическое
строение" и "симметрия Td" не
идентичны. Например, молекула хлороформа CHCl3
имеет тетраэдрическое строение, однако ее
симметрия не является тетраэдрической; она
принадлежит к группе C3v (как аммиак), а не к
группе Td.
|